WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Pakken koffie

Goedemiddag ik kreeg een vraag maar kom er niet helemaal uit.

Beschouw pakken koffie met μ = 245 gram en  = 6 gram. Op de pakken koffie staat “inhoud 250 gram”. Volgens de Europese regelgeving mag dan hoogstens 4% van alle pakken minder dan de op het pak beloofde 250 gram koffie bevatten.

a. Toon met een berekening aan dat er bij deze instelling van de vulmachine niet aan de Europese regelgeving wordt voldaan.

b. Bepaal de populatiewaarde waarvoor geldt dat er 4% van alle pakken minder dan deze waarde bedragen. Wat kan u dan besluiten over een nieuwe instelling die gezet moet worden op de machine om toch aan de Europese norm te voldoen?

Voor het beantwoorden van vraag a denk ik dat ik deze kan berekenen met Excel: =norm.verd(245;250;6;1) en komt dan op een antwoord van 0,202328381 uit dus naar mijn mening 20%. Weet niet of ik het goed zie. Maar snap niet zo goed hoe ik vraag B kan beantwoorden. mogelijk dat jullie mij hierbij kunnen helpen.
Jade
Ouder - vrijdag 6 januari 2023

Antwoord

Hallo Jade,

Jouw uitkomst van 0,202328381 betekent dat (afgerond) 20% van de pakken een gewicht heeft van minstens 250 gram, dus 80% van de pakken is te licht. Dat is aanzienlijk meer dan de toegestane 4%.

Om ervoor te zorgen dat slechts 4% van de pakken te licht is, moet het gemiddelde gewicht $\mu$ hoger dan 250 gram worden gekozen, zoals te zien in de onderstaande figuur:

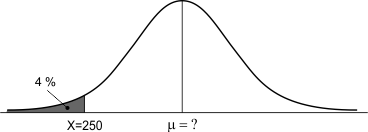
Het gemiddelde gewicht $\mu$ moet zodanig worden gekozen dat slechts 4% van de pakken lichter is dan 250 gram. In Excel kunnen we de afstand tussen X en $\mu$ niet voor een willekeurige normaal verdeelde variabele berekenen. We kunnen dit wel bij een standaardnormale verdeling, d.w.z. een normale verdeling met gemiddelde $\mu$=0 en standaardafwijking $\sigma$=1, zie de figuur hieronder. De afstand van $\mu$ naar X wordt Z genoemd (zie Wikipedia: Z-score):

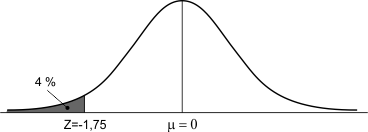
Met de functie NORM.S.INV(0.04) vinden we Z=-1,75. Dat betekent: de waarde X ligt 1,75 keer de standaardafwijking links van het gemiddelde $\mu$.
Voor de eigenlijke vaag rekenen we deze Z-score terug naar een gevraagde waarde van $\mu$ met de formule:

Z = ^(X-$\mu$)/_$\sigma$
-1,75 = ^(250-$\mu$)/₆

Oplossen van deze vergelijking levert $\mu$=260,5 gram.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 6 januari 2023