WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Ellips

Beste,

Ik moet mijn vriendin helpen bij een oefening maar snap het spijtig genoeg zelf ook niet. Ik had haar beloofd om tegen morgen het te kunnen uitleggen maar mijn probleem is eerder dat ik de stappen ervan niet kan. Zou u mij hierbij kunnen helpen?

Op een ellips & nemen we op de grote as en aan dezelfde kant van het middelpunt het brandpunt F en de top P. De loodlijn in F op de grote as snijdt & in Q en Q'. We nemen ook nog een willekeurig punt De8 met D +P en noemen D zijn projectie op de grote as. Bewijs dat de oppervlakte van een vierkant met zijde | DD'| kleiner is dan de oppervlakte van een rechthoek met afmetingen | QQ'I en | PD'l.

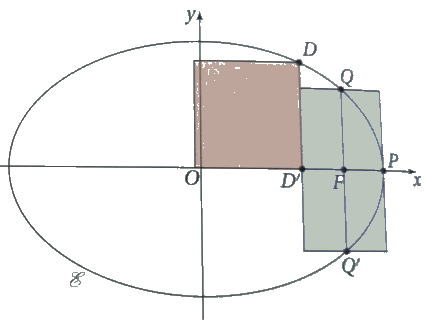
Ik stuur hierbij dan ook via email hoe het eruit ziet.
Dank je wel voor uw tijd.
Amber
3de graad ASO - dinsdag 24 augustus 2021

Antwoord

Je kunt het het makkelijkst met behulp van de vergelijking
$$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1
$$doen. Er geldt $P=(a,0)$ en $F=(c,0)$ (er geldt $a^2=b^2+c^2$). Verder schrijven we $D'=(x,0)$ en $D=(x,y)$.

Dus
$$(DD')^2=y^2=\frac{b^2}{a^2}(a^2-x^2) = \frac{b^2}{a^2}(a-x)(a+x) \qquad(*)
$$Verder $PD=a-x$ en
$$PQ^2=\frac{b^2}{a^2}(a^2-c^2)=\frac{b^4}{a^2}
$$en dus $PQ=\frac{b^2}{a}$.

De oppervlakte van de rechthoek is dan
$$2\cdot PD\cdot PQ=2\frac{b^2}{a}(a-x)=\frac{b^2}{a^2}(a-x)\cdot2a \qquad(**)
$$Vergelijk nu de uitdrukkingen in $(*)$ en $(**)$ maar eens.

kphart

Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 27 augustus 2021