WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Twee manieren

Beste

Kan u aub mij met deze vraag helpen.

Ik moet deze vraag op 2 manieren kunnen doen. Ik heb met integralen kunnen doen maar ik weet niet hoe ik ze moet tekenen en zelfde antwoord krijgen.

Mijn antwoord op eerste manier is 10.5

Amber
3de graad ASO - woensdag 11 augustus 2021

Antwoord

Hallo Amber,

Heb je al een schets van de grafiek gemaakt? Vast niet, want anders had je gezien dat een gedeelte van de bedoelde oppervlakte onder de x-as ligt. Integreren over dit deel levert dan een negatieve waarde op, terwijl de oppervlakte zelf natuurlijk alleen positief kan zijn. Voor het bepalen van een oppervlakte moet je de delen boven de x-as en onder de x-as apart nemen, en de min-tekens bij oppervlaktes onder de x-as negeren.

Hieronder zie je de schets:

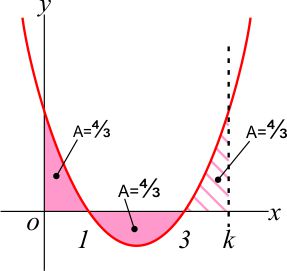
De gekleurde oppervlakte bestaat uit 3 delen:
Van x=0 tot x=1. Ga voor jezelf na dat deze oppervlakte gelijk is aan ⁴/₃
Van x=1 tot x=3. Ga voor jezelf na dat de uitkomst van de integraal gelijk is aan -⁴/₃. De gekleurde oppervlakte is dus ⁴/₃
Van x=3 tot x=k. Om de totale oppervlakte gelijk te maken aan 4, moet dit deel gelijk zijn aan ⁴/₃. Ofwel:
[¹/₃x³-2x²+3x] voor x=3 tot x=k =⁴/₃
Je kunt deze integraal netjes uitwerken (vooral doen, goede oefening), maar in de schets zie je dat deze gestreepte oppervlakte er precies zo uitziet als de oppervlakte tussen x=0 en x=1. Je kunt dus wel 'raden' dat de uitkomst is: k=4.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 12 augustus 2021