WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Constructieproblemen met transformaties

Hallo team WisFaq

Voor wiskunde zijn we bezig geweest met transformaties en het oplossen van vraagstukken a.d.h.v. transformaties. Ik zat vast met volgend vraagstuk:

Er is een rechte r gegeven en twee punten X en Y die zich aan dezelfde kant van de rechte r bevinden. Construeer een punt Z op r zodanig dat de scherpe hoek XZ en r dubbel zo groot is als de scherpe hoek tussen YZ en r.

Ik ben begonnen met het tekenen van het spiegelbeeld van Y en heb die verbonden met X. Ik weet dat ik nog een ander punt nodig heb die op r ligt, maar weet niet hoe ik die moet vinden.

Ik zou het erg appreciëren als jullie me verder kunnen helpen.

Alvast bedankt.
Groetjes
Joke
Joke v
3de graad ASO - dinsdag 18 mei 2021

Antwoord

Hallo Joke,

Er zijn vast vele manieren voor deze constructie, maar ik zou gebruik maken van een "cirkel van Apollonius", zie eventueel de link onderaan.

Dat kan als volgt: Snijd $XY$ met $r$, snijpunt $E$. Ik ga er even van uit dat $X$ tussen $E$ en $Y$ ligt.

Je wil nu natuurlijk een punt $F$ op $r$ hebben zodat $FX$ de bissectrice is van $FE=r$ en $FY$.

Daarvoor maken we de bijbehorende cirkel van Apollonius als volgt: ik snij de cirkels met middelpunt $E$ en straal $2\cdot EX$ en de cirkel met middelpunt $Y$ en straal $2 \cdot XY$. De snijpunten zijn $P$ en $Q$. De cirkel door $P$, $Q$ en $X$ is nu de gezochte cirkel van Apollonius. Voor elk punt $F$ op deze cirkel is $FX$ bissectrice van $FE$ en $FY$.

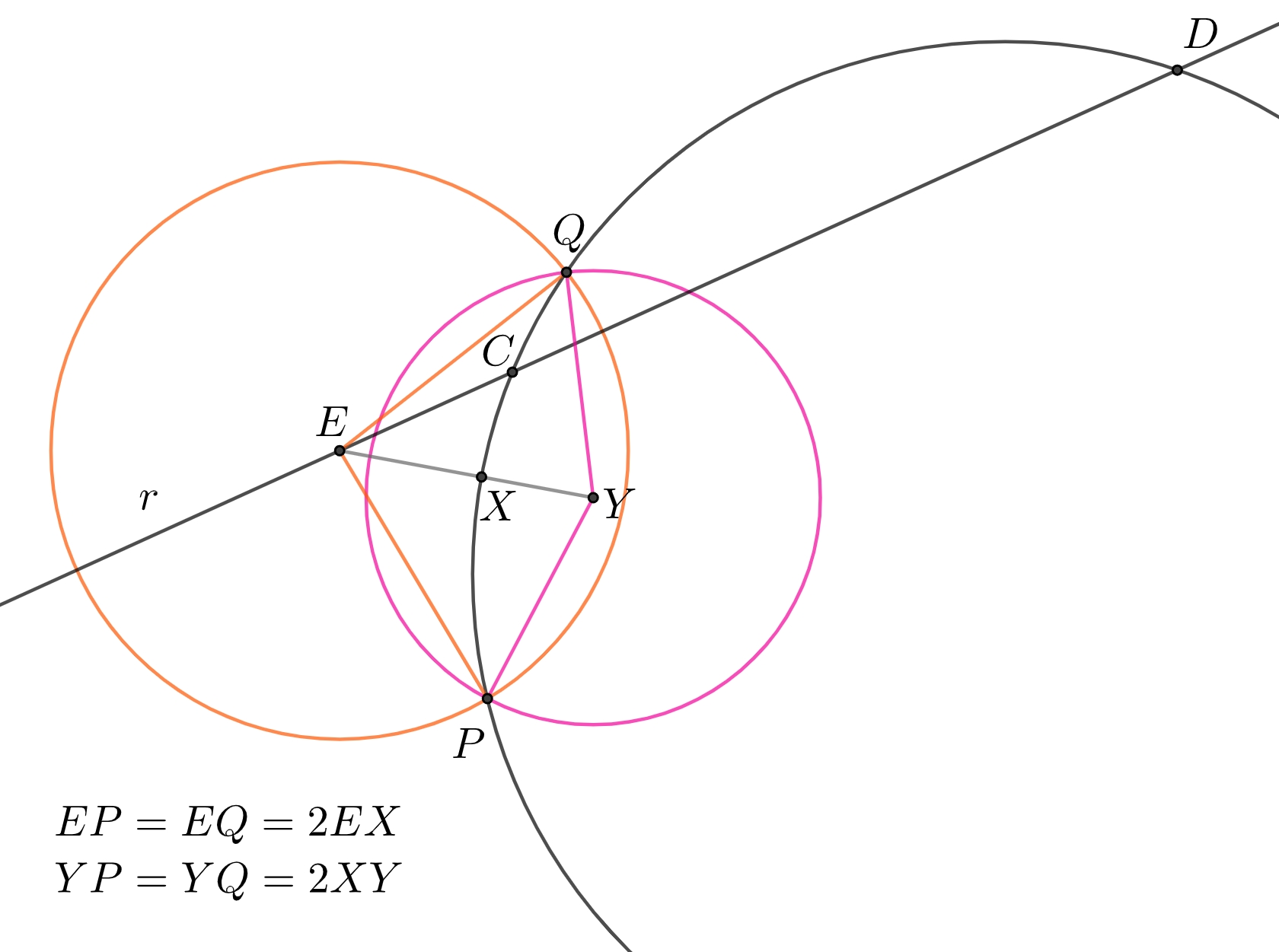
In het bijzonder geldt dat voor de snijpunten $C$ en $D$ van deze cirkel met $r$. Maar $C$ valt in mijn figuur af (waarom?).

Kun je hiermee verder?

Met vriendelijke groet,
Zie Wikipedia: Cirkel van Apollonius

Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 18 mei 2021