|
|
|
\require{AMSmath}



Re: Re: Pi of 2pi
2018 tijdvak 2 vraag 13
Tessa
Leerling bovenbouw havo-vwo - zaterdag 8 mei 2021
Antwoord
't Zou handig zijn te vermelden dat het om VWO wiskunde B gaat...
Er staat in het correctievoorschrift:
$
\left| {\sin (2t)} \right| = \frac{1}
{2}
$ geeft $
2t = \frac{1}
{6}\pi + k \cdot \pi \vee 2t = \frac{5}
{6}\pi + k \cdot \pi
$
Dat klopt wel...!
$
\eqalign{
& \left| {\sin (2t)} \right| = \frac{1}
{2} \cr
& \sin (2t) = \frac{1}
{2} \vee \sin (2t) = - \frac{1}
{2} \cr
& 2t = \frac{1}
{6}\pi + k \cdot 2\pi \vee 2t = \frac{5}
{6}\pi + k \cdot 2\pi \vee 2t = 1\frac{1}
{6}\pi + k \cdot 2\pi \vee 2t = 1\frac{5}
{6}\pi + k \cdot 2\pi \cr
& 2t = \frac{1}
{6}\pi + k \cdot 2\pi \vee 2t = 1\frac{1}
{6}\pi + k \cdot 2\pi \to 2t = \frac{1}
{6}\pi + k \cdot \pi \cr
& 2t = \frac{5}
{6}\pi + k \cdot 2\pi \vee 2t = 1\frac{5}
{6}\pi + k \cdot 2\pi \to 2t = \frac{5}
{6}\pi + k \cdot \pi \cr}
$
Je ziet dat er absoluutstrepen staan. Dat is wel van belang. Als je die 'wegwerkt' krijg je 'vier oplossing', die je paarsgewijs bij elkaar kan bossen...
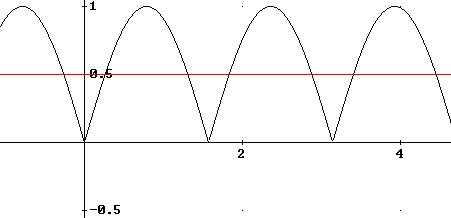
Hopelijk is het nu helderder...
Zie Wiskunde B vwo 2018 tijdvak 2

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 8 mei 2021
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|








 Dit is een reactie op vraag 92148
Dit is een reactie op vraag 92148 


