|
|
|
\require{AMSmath}
Integreren goniometrische veelterm
Goede avond,
Gegeven:
I=((4-cos2x+2cosx-sinx))dx/(2+cosx)2
Substutie geprobeerd, ook splitsing van termen.Ik geraak niet vertrokken.Vilgensd wxolfram is het een moeilijk en lang eindresultaat....
Enkele hints zouden welkom zijn.
Groeten
Rik Le
Iets anders - woensdag 5 mei 2021
Antwoord
Een standaardsubstitutie in dit geval is u=\tan\frac x2, ofwel x=2\arctan u.
Dan verandert dx in \frac2{1+u^2}\,du.
Verder geldt natuurlijk \cos x=\cos^2\frac x2-\sin^2\frac x2, en \sin x=2\sin\frac x2\,\cos\frac x2.
Hoe helpt dit?
Welnu, bekijk dit plaatje
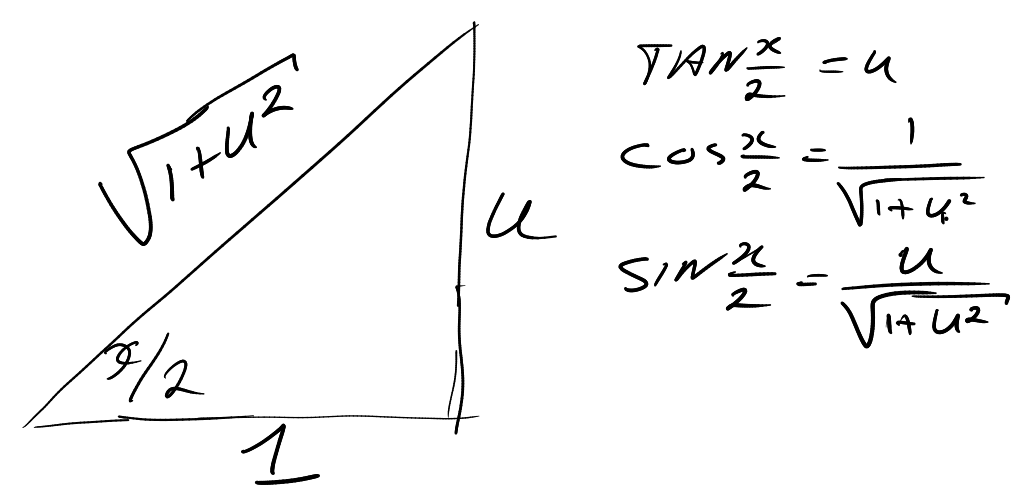
Nu volgt
\cos x= \frac{1-u^2}{1+u^2}\text{ en }\sin x=\frac{2u}{1+u^2} Als je dit netjes invult en uitwerkt krijg je een quotiënt van twee polynomen dat je met behulp van breuksplitsen etc kunt primitiveren, waarna invullen van u=\tan\frac x2 de gewenste primitieve oplevert.
kphart
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 5 mei 2021
|
|
home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2025 WisFaq - versie 3
|
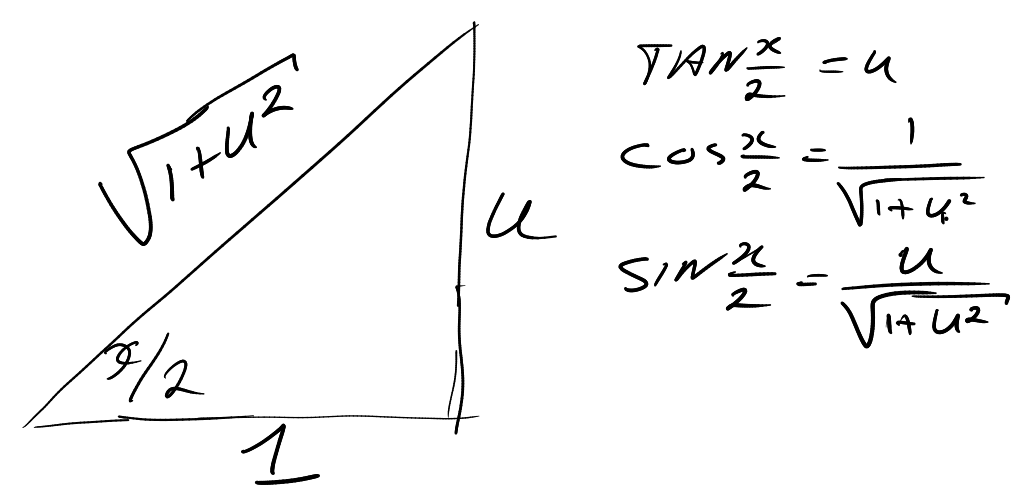
Re: Integreren goniometrische veelterm