WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Hefboom, steunpunten en macht

Goede middag,

Ik zit met een probleem aangaande afgeleiden dat meer naar de fysica zou kunnen ruiken. Toch komt hier mijn probleem.

Aan een hefboom hangt, tussen steunpunt en macht, een last van 50 kg. Die last hangt op 50 cm van het steunpunt en gewicht van de hefboom is 2 kg.
Bepaal de lengte van de hefboom zodat de macht maximaal wordt.
IK zou graag een voorstelling krijgen van de gevraagde functie f(x)=......, die ik dan wel zelf verder zal kunnen afleiden en oplossen. Hoop ik toch.
Sorry voor de last (eigenlijk fysicavraag)
Groetjes
Rik Le
Iets anders - vrijdag 26 maart 2021

Antwoord

Hallo Rik,

Als ik het goed begrijp, gaat het om deze situatie:

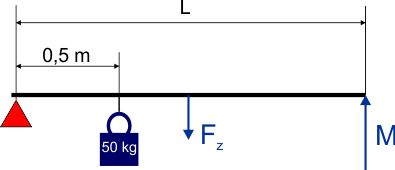
In dit plaatje is F_z de zwaartekracht werkend op de hefboom van 2 kg, M is de macht (kracht die de hefboom in evenwicht houdt). Het rode driehoekje geeft het steunpunt weer.
In dat geval werken ten opzichte van het steunpunt twee momenten rechtsom: het moment als gevolg van de zwaartekracht op de last van 50 kg en het moment als gevolg van F_z. Voor het moment rechtsom geldt:

M_r = 50·g·0,5 + 2·g·^L/₂
M_r = 25·g + g·L

Hierin is g de gravitatieversnelling.

De macht M levert een moment linksom:

M_l = M·g·L

In geval van evenwicht geldt:

M_l = M_r
M·g·L = 25·g + g·L
M = ^(25+L)/_L

Echter, dit is een continu dalende functie. Dat is ook wel te begrijpen: naarmate de hefboom langer wordt, is aan het uiteinde steeds minder kracht nodig om de last te dragen. Andersom: hoe korter de hefboom, hoe groter de macht. Je zult dus geel lengte vinden waarbij de macht maximaal wordt.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 27 maart 2021

Re: Hefboom, steunpunten en macht