|
|
|
\require{AMSmath}



De standaarddeviatie berekenen
Uit resultaten van een kwaliteitscontrole blijkt dat 94.52% van de meetwaarden onder de 1.250 ml ligt. Verder is bekend dat 86.21% boven de 650 ml ligt.- Hoe groot is het gemiddelde en de standdaarddeviatie?
Ik heb geen GR of app ter beschikking. $\mu$ kan ik berekenen en is 950 ml. Alleen wat is $\sigma$?
Elijah
Leerling mbo - woensdag 3 maart 2021
Antwoord
Ik denk niet dat die $\mu=950$ klopt. Wat je moet doen is opzoeken welke $z$-scores horen bij die 94.52% en die 86.21%. Dat kan met de tabel:
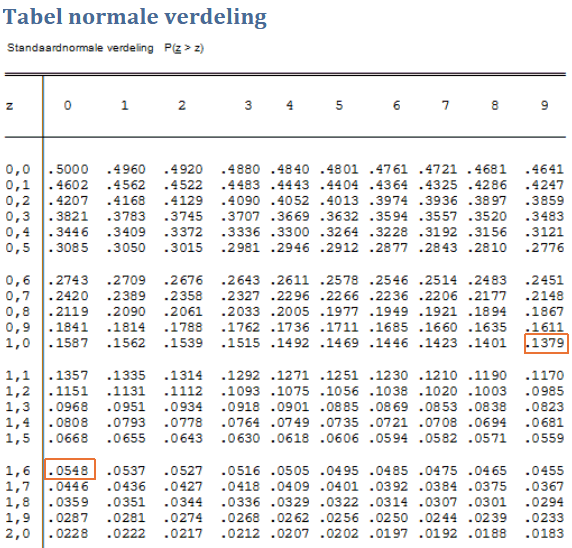
Je kunt zien dat de 650 en 1250 niet symmetrisch liggen ten opzichte van het gemiddelde. Dat was ook niet gegeven. Je moet nog wel de percentages vertalen voor het gebruik van de 'halve tabel'. Kijk maar 's goed!
Wat je moet doen is twee keer de formule voor de normale verdeling gebruiken. Vul in wat je weet en je krijgt dan een stelsel van twee vergelijkingen met twee onbekenden, de $\mu$ (mu) en $\sigma$ (sigma) dus...
$
\eqalign{
& \frac{{650 - \mu }}
{\sigma } = - 1,09 \cr
& \frac{{1250 - \mu }}
{\sigma } = 1,6 \cr
& ... \cr
& \mu \approx 893 \cr
& \sigma \approx 223 \cr}
$
Als je dat oplost dan heb je de $\mu$ en $\sigma$ te pakken. Zou dat lukken?

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 3 maart 2021
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|










