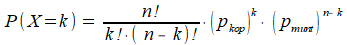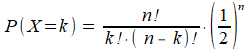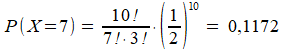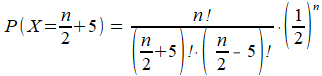WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Kansberekening in de oneindigheid

Dit is een reactie op vraag 91425

Ik ben met een computerprogramma bezig en zit alweer met de volgende vraag. Mijn programma kan niet oneindig een munt opgooien omdat deze gelimiteerd is (voor nu in ieder geval) door een variabele van het type 'long', dit wil zeggen dat mijn programma maximaal 9,223,372,036,854,775,808 keer een muntje kan opgooien.

Nu is mijn volgende vraag:als ik 10 meer kop wil gooien dan munt, wat is dan de kans (1 op hoeveel (afgerond naar hele getallen)) dat dat na het maximaal aantal wat mijn programma kan gooien:niet lukt. Ik ben dus programmeur en weet niet bijzonder veel van wiskunde, graag ontvang ik hier wat hulp bij, en ook uitleg over de berekening alstublieft.

Verder vroeg ik mij af hoe de berekeningen in elkaar zitten om bijvoorbeeld te berekenen hoeveel keer gooien nodig is voor 75% kans op 4 keer meer kop.

Of bijvoorbeeld 60% kans op 7 keer meer kop. Ik snap er net iets te weinig van om dit om te zetten in een formule. Ik heb dit nooit gehad op school (er wordt op mijn hbo-informatica helemaal niets gedaan aan wiskunde), en vraag me ook af of dit soort onderwerpen wel gegeven worden op school of kom je dan echt uit bij een wiskundige opleiding?

Graag ontvang ik antwoord op mijn vragen. Dankuwel alvast, met vriendelijke groet
Paul S
Student hbo - woensdag 27 januari 2021

Antwoord

Hallo Paul,

Wanneer je een aantal keer een muntje opgooit en je telt het aantal keer dat je kop gooit, dan heb je te maken met een binomiale verdeling.

Stel de kans op kop is p_kop, de kans op munt is p_munt. We gooien n keer, we noemen X het aantal keer dat je kop gooit. De kans dat X (dus: het aantal keer kop) gelijk is aan een zekere gekozen waarde k, dan bereken je de kans P(X=k) op deze gebeurtenis met:

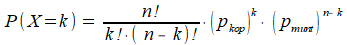
Bij een eerlijk muntje geldt p_kop = p_munt = ¹/₂. De formule is dan te vereenvoudigen tot:

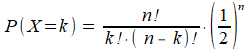
Ik geef een eenvoudig voorbeeld:

Stel je gooit 10 keer, dus n=10. De kans op 7 keer kop bereken je met:

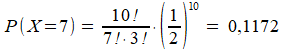
Wanneer je n keer gooit, en je wilt 10 keer meer kop dan munt, dan wil je kennelijk ⁿ/₂+5 keer kop en daarmee ⁿ/₂-5 keer munt. Netjes invullen van de formule levert je de kans dat dit gebeurt:

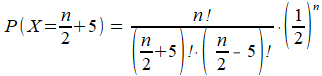
Met deze formule kan je onderzoeken hoeveel keer je moet gooien (dus: wat de waarde van n moet zijn) om de kans op 10 keer meer kop dan munt te berekenen, en soortgelijke vragen beantwoorden die je noemt.

Let wel: met deze formule bereken je de kans op precies 10 keer meer kop dan munt. Wellicht wil je de kans weten op minstens 10 keer meer kop dan munt.

Eigenlijk moet je dan de kansen berekenen op precies 10 keer meer, precies 11 keer meer, precies 12 keer meer enz. Met een handige strategie kan je een veelheid van berekeningen wel vermijden: je kunt bijvoorbeeld de kansen berekenen op uitkomsten waarbij het verschil tussen aantal keer kop en aantal keer munt juist kleiner is dan 10. De kans dat dit verschil minstens 10 is, vind je door de berekende kans van 1 af te trekken. De helft hiervan is dan de kans dat het aantal keer kop groter is dan het aantal keer munt. Kortom: definieer je vragen heel zorgvuldig, verzin vervolgens een strategie die precies past op de gestelde vraag.

Je zult wel tegen meer praktische problemen oplopen. Voor grote waarden van n neemt n! snel toe. Wellicht moet je een handige strategie bedenken om de breuk in de formule te berekenen. Een mooie uitdaging voor een programmeur.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 29 januari 2021

Re: Re: Kansberekening in de oneindigheid