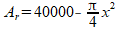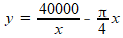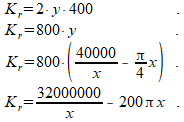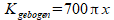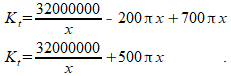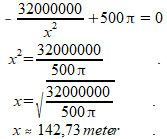WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Re: Re: Re: Toegepaste differentiaalrekenen

Dit is een reactie op vraag 90276

Beste,

Oke da heeft mij verduidelijkt, die dubbele variabele werkt best bij gekoppelde snelheden neem ik aan.

Dus als ik zo een beetje alles begrijp de formule van de ene zijde is 40.000- 1/4x²$\pi$(dus de zijden van de halve cirkel die ook de breedte is van de rechthoek) en de rechte zijde van het rechthoek is (40.000/x)-1/4x$\pi$, en om die onbekende weg te werken neem ik de afgeleiden van de rechte zijde dus dat wordt (-40.000/x²)-$\pi$/4 dat stel ik gelijk aan 0 om de kritische punten te vinden van het minimale afmetingen te vinden, ik kom uit op ongeveer 225,67m voor de x waar het mij nie helemaal logisch klinkt dan de diameter van de halve cirkel of de rechte zijde van rechthoek :(
Steeve
Student universiteit België - dinsdag 21 juli 2020

Antwoord

Hallo Steeve,

Je vergeet dat de lengte van de cirkelbogen ook meetellen bij de totale omtrek, en je vergeet dat je de kosten moet minimaliseren, niet alleen de zijde y. Probeer te werken volgens een overzichtelijke structuur:

Oppervlakte station: A=40.000 m²
Stel breedte x.
Oppervlakte halfcirkelvormige delen: A_c=^$\pi$/₄·x²
Dan blijft over voor de oppervlakte van de rechthoek:

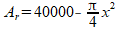
A_r=x·y, dus y=A_r/x

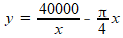
Kosten K_r rechte stukken (2y) zijn €400,- per meter, dus:

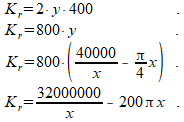
Lengte gebogen stukken: $\pi$·x, kosten: €700,- per meter, dus:

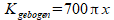
Totale kosten K_t:

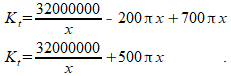
Hiervan willen we het minimum berekenen, dus:
K_t'=0

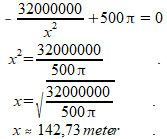
Vul deze waarde in de formule van K_t in om de minimale kosten te vinden.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 21 juli 2020