|
|
|
\require{AMSmath}



Vlak en hoek in een piramide
Bij opgave 4 van een oud examen:
In een regelmatige vierzijdige piramide T.ABCD zijn alle ribben even lang. Het midden van de ribbe CT is het punt P. Neem AB = 8 cm.- Construeer in een stereometrische figuur van de piramide de doorsnede van de piramide met het vlak dat door A en P gaat en dat evenwijdig aan BT is.
- Bereken hoek BPD
Kom ik niet helemaal uit door de manier hoe het uitgewerkt wordt.
Ze vragen een vlak te tekenen in een figuur die door het midden gaat van CT en evenwijdig aan BT. Ik snap dat ze de lijn PS1 dan tekenen die is evenwijdig aan BT. S2 snap ik ook wel. Daar laten ze DC en AS1 snijden om het vlak te tekenen maar ik weet niet of ik zo'n vlak alleen kan tekenen bij een volgende opgave.
De hoek BPD berekenen kom ik ook niet helemaal uit. Hoe komen ze aan BP? Ze nemen alle zijden 2 de zijde BS1 nemen ze 1 maar de zijde PS1=2. Dit snap ik niet. Ik snap dat het midden is van BD en BS √2 is. Dan nemen ze hoek BPD maar dat is volgens mij sinBPD=1/2 dat zie ik niet zo goed.
Alvast bedankt.
mboudd
Leerling bovenbouw havo-vwo - dinsdag 19 mei 2020
Antwoord
Op Tekenen van doorsneden kan je een aantal oefeningen vinden. Ik heb daar nog ergens uitleg van.
Voor de tweede vraag moet je (zoals altijd!) de figuren waarin je iets wilt berekenen even apart in het platte vlak tekenen. Kijk goed naar de gegevens.
Bij b. gaat het om driehoek BPD.
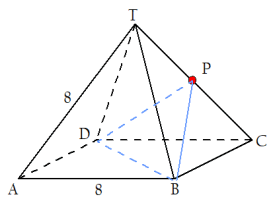
De kunst is nu om de afmetingen van zijden van driehoek BPD te bepalen.
Gebruik:
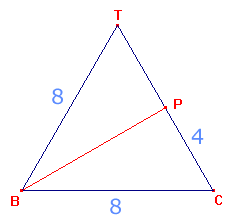
en dan:
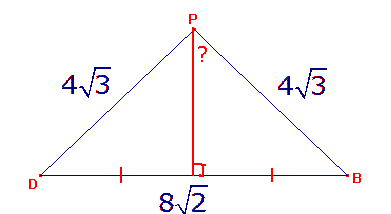
...en dan kan je hoek BPD wel bepalen denk ik.

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 20 mei 2020
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|













 Re: Vlak en hoek in een piramide
Re: Vlak en hoek in een piramide