WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Differentievergelijking

Hoi, ik heb deze opgave die ik moet maken, maar ik kom er niet helemaal uit:
Stel Pn+1= 1,3·Pn·(1−Pn)met P0= 0,4.
Onderzoek of de rij bij deze differentievergelijking convergeert of divergeert en berekende eventuele grenswaarde. Geef ook een directe formule als het hier om een lineaire differentievergelijking gaat.

ik ben er al uitgekomen dat er sprake is van een kwadratische differentievergelijking van de eerste orde.
Om te kijken of er sprake is van convergeren of divergeren plot ik een webgrafiek.
GR:
nmin = 0
u(n+1)=1,3u(n)·(1-u(n))
u(0) = 0,4

Je krijgt dan een parabool met een lineaire lijn. Als ik het goed heb is het dan convergerend.
Hoe je dan precies de grenswaarde moet berekenen met een goede notatie weet ik niet.
Ik zie namelijk wel dat P steeds de waarde 0,2307692 heeft (ongeveer). Dit zie ik in de tabel op de GR.
Maar hoe kan je de grenswaarde berekenen en is deze waarde die ik heb wel goed (als grenswaarde of moet dit een breuk zijn?)?

jonas
Leerling bovenbouw havo-vwo - woensdag 6 mei 2020

Antwoord

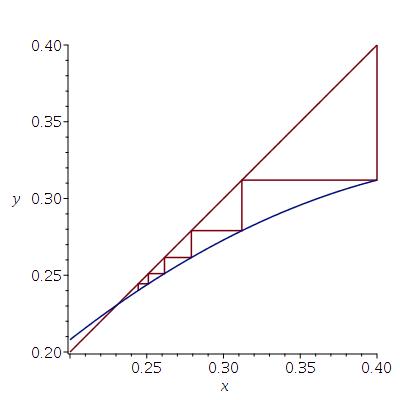
Kijk naar de grafiek van de lijn $y=x$ en de grafiek van $f(x)=1.3\cdot x\cdot(1-x)$, voorbij het snijpunt, bij $x=3/13$ (reken maar na) geldt $x > f(x) >3/13$ Omdat $0.4 > 3/13$ volgt dat met $p_0=0.4$ je krijgt dat $p_0>p_1>3/13$, en $p_1>p_2>3/13$, enzovoort. Je rij daalt en is ligt altijd boven $3/13$. Hij convergeert naar de $x$-waarde van het snijpunt.

kphart

Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 6 mei 2020