WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Staaf in een vat

Een staaf van 1,2m rust op de rand van een vat. Het vat heeft de vorm van een halve bol met d=90cm. Als men de staaf loslaat zal de staaf glijden tot het midden zo laag mogelijk ligt. maw. de afstand van het midden tot het steunvlak is minimaal.
welke hoek maakt de staaf dan met de bovenrand
bepaal de laagste positie van het midden tov het steunvlak
Het steunvlak komt overeen met de bodem van het vat.

De hoek die heb ik gevonden door de nulpunten te bepalen uit de afgeleide van de functie y=45sin2x-60sinx y is hierbij de afstand van het midden tot de bovenrand. de hoek komt overeen met 26°4'

Het probleem is nu dat ik eigenlijk een functie moest hebben die de hoogte van het steunvlak tot het midden bepaalt en niet van de bovenrand tot het midden. Met driehoeksmeetkunde dacht ik ook makkelijk de hoogte van het midden tot het steunvlak te kunnen bepalen. Maar deze uitkomst komt niet overeen met de uitkomst van de oplossingen.
Iemand een idee hoe je deze functie moet bepalen?
Alvast bedankt.
jonath
Student Hoger Onderwijs België - zaterdag 1 september 2018

Antwoord

Hallo Jonathan,

Als ik het goed begrijp, is dit de situatie:

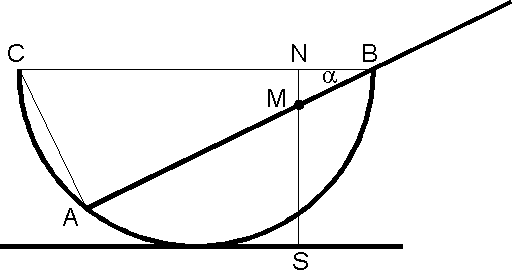
Je hebt het volgende al gevonden:

Hoek CAB is 90° (stelling van Thales), CB=90 cm, dus AB=90cos$\alpha$.
AM=60, dus MB=90cos$\alpha$ - 60.

Dan geldt:
MN=MBsin$\alpha$
MN=90sin$\alpha$·cos$\alpha$ - 60sin$\alpha$
MN=45sin2$\alpha$ - 60sin$\alpha$

De laatste stap om SM te berekenen is in feite heel eenvoudig:
SN is gelijk aan de straal van de bol, dus SN=45 cm.
Dan blijft over voor SM:

SM=SN-MN
SM=45 - (45sin2$\alpha$ - 60sin$\alpha$)
SM=45 - 45sin2$\alpha$ + 60sin$\alpha$

Op zich is deze stap niet nodig: wanneer je d.m.v. differentiëren het maximum van MN hebt gevonden, heb je automatisch het minimum van SM. Je vindt dit minimum bij dezelfde hoek $\alpha$=26°4'.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 2 september 2018