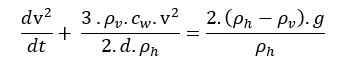WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Constante coefficienten

Ik heb de volgende differentiaalvergelijking

dv²/dt + (3.c.y)/(2d) = 2.e

hierbij is c,d en e een bekende van densiteiten maar makkelijker om het hier zo te schrijven.

Toon dit aan door middel van de oplossingsmethode voor een lineaire differentiaalvergelijking met constante coëfficiënten (met andere woorden algemene oplossing van de homogene vergelijking (=zonder tweede lid) plus particuliere oplossing van de differentiaalvergelijking met tweede lid.

In dit geval is de algemene oplossing een exponentieel dalende functie en de particuliere oplossing de constante uitdrukking voor

Het is nodig/nuttig aan te geven hoe snel die exponentieel dalende functie uitsterft.
kim
Student universiteit België - dinsdag 13 februari 2018

Antwoord

De oorspronkelijke vergelijking was

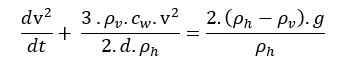
Ik zou die vergelijking eerst even vereenvoudigen tot
$$
\frac{\mathrm{d}y}{\mathrm{d}t}+ay=b
$$met $y=v^2$, en $a=3\rho_\nu c_w/(2d\rho_h)$ en $b=2(\rho_h-\rho_\nu)g/\rho_h$ dus. Dat is wat overzichtelijker.
De bijbehorende homogene vergelijking is $y'+ay=0$ en die heeft $y=C\mathrm{e}^{-at}$ als oplossing.
Een particuliere oplossing kun je bijna direct zien: $a$ en $b$ zijn constant, dus je kunt een constante functie proberen en, inderdaad, $y_p(t)=b/a$ is een oplossing.
De algemene oplossing is dus
$$
y(t)=\frac ba+ C\mathrm{e}^{-at}
$$Nu kun je weer invullen wat $a$ en $b$ waren en kijken of je die kwalitatieve vragen kunt beantwoorden.

kphart

Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 14 februari 2018