WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Verlichtingssterkte tafel

Een lamp van 60 W hangt 0,8 m boven het midden van een ronde tafel met diameter 1,20 m. De lichtintensiteit naar het midden van de tafel bedraagt 60 cd en naar de rand van de tafel 65 cd. Hoe groot is de verlichtingssterkte in het midden van de tafel en op de tafelrand?
(antwoord: Emidden = 94 lx, Ehoeken = 52 lx)

Ik weet hoe je Emidden berekend maar weet iemand hoe je aan Ehoeken = 52 lx kan komen?
Mike
Student Hoger Onderwijs België - woensdag 17 januari 2018

Antwoord

Hallo Mike,

Eerst maar even een schets van de situatie:

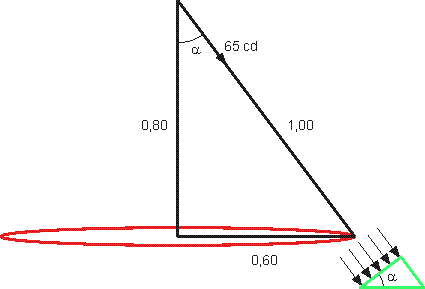
De lamp in de tophoek zendt licht uit richting rand van de tafel met een intensiteit van 65 cd. Met behulp van pythagoras kan je berekenen dat de afstand tot de rand van de tafel 1 meter bedraagt. Op die afstand is de verlichtingssterkte op een oppervlak loodrecht op de lichtbundel dan:

E_loodrecht = ⁶⁵/_(1²) = 65 lux.

De verlichtingssterkte op de schuine zijde van het groene driehoekje zou dus 65 lux zijn. In werkelijkheid verdeelt dit licht zich over een groter, horizontaal oppervlak (de horizontale zijde van dit driehoekje). De grootte van dit horizontale oppervlak is ¹/_{cos($\alpha$)} keer zo groot. We moeten de oorspronkelijke verlichtingssterkte van 65 lux dus delen door deze ¹/_{cos($\alpha$)}. Voor de verlichtingssterkte op de rand van de tafel vinden we dan:

E_{rand tafel}=65·cos($\alpha$)

De hoek $\alpha$ vinden we ook terug in de grote zwarte driehoek. In deze grote driehoek zien we:

cos($\alpha$) = ^0,80/_1,00 = 0,8

Dus:

E_{rand tafel} = 65·0,8 = 52 lux.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 17 januari 2018