WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Percentiel

Gegeven: een kansveranderlijke X volgt N(50;10)'
-Geef het percentiel dat hoort bij 38
-Geef de z-waarde en de x-waarde die horen bij Q(0,67)

Ik kan hier niet aan beginnen en weet nizt welke formules ik moet gebruiken. Ik dacht eerst de z-waarde van 38 te zoeken, maar dan kom ik op -0,31 en dat in te vullen in: u+z·o maar dan kom ik iets verkeerd uit. De uitkomt zou 12 moeten zijn voor het percentiel, 0,44 voor de z-waarde en 54 voor de x-waarde.
sarah
Student Hoger Onderwijs België - woensdag 17 januari 2018

Antwoord

Hallo Sarah,

Om inzicht te krijgen in vragen over de normaalverdeling is het handig om een schets te maken:

Teken de normaalkromme, geef gemiddelde en standaardafwijking aan, geef de grenzen aan die een relevant gebied onder de kromme insluiten (vaak ligt één van de grenzen in het oneindige) en arceer dit relevante gebied. In dit geval ziet die schets er zo uit:

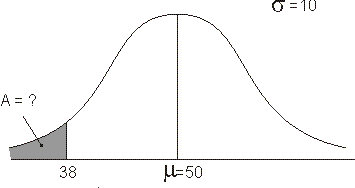
Gevraagd wordt de oppervlakte A van het grijze gebied (en dan vermenigvuldigen met 100 om hiervan een percentiel te maken). Je kunt deze oppervlakte berekenen als de linker- en rechter grens hiervan bekend zijn, het gemiddelde en de standaardafwijking. Gebruik hiervoor een grafische rekenmachine, een rekenprogramma (bv Excel), of een hulpje zoals hieronder:
Je kunt ook gebruik maken van een tabel. Hiervoor moet je de vraag eerst transformeren naar een standaardnormaalverdeling. We maken een nieuwe variabele Z volgens:

Z=(x-$\mu$)/$\sigma$

Voor x=38 wordt dit:

Z = (38-50)/10 = -1,2

Hiermee wordt de vraag 'vertaald' naar:

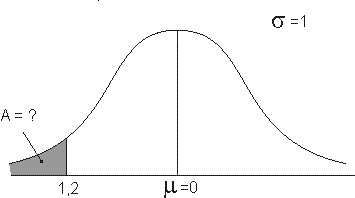
Met behulp van een tabel of een rekenapparaat vinden we: A$\approx$0,115. Dit komt overeen met een percentiel van 11,5 (afgerond op gehelen: 12).

Dan de tweede vraag. Als we uitgaan van een standaardnormaalverdeling, dan ziet de bijbehorende schets er zo uit:

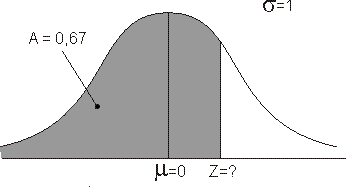
Met behulp van een tabel (of een rekentool) vinden we: Z$\approx$0,4399

Deze Z-waarde geeft aan wat het verschil is tussen een waarde x en het gemiddelde, uitgedrukt in een aantal keer de standaardafwijking. De schets voor de oorspronkelijke variabele x ziet er dan zo uit:

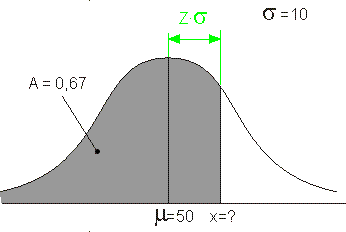
De standaardafwijking is 10, dus Z·$\sigma\approx$4,399. De gevraagde waarde van x wordt dan:

x=50+4,399$\approx$54

Hierin herken je ook weer de transformatie-formule:

Z=(x-$\mu$)/$\sigma$

dus:

x=Z·$\sigma$+$\mu$

Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 18 januari 2018