WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

De Z-waarde (99%) berekenen

Hoe bereken je de z99% waarde als $\sigma$= 16, gemiddelde steekproef = 509,5 en de standaardafwijking van het gemiddelde = 0,5060, N = 1000. In mijn syllabus wordt deze zo berekend:
P(µ-a.$\sigma<$X$<$µ+a$\sigma$)=0,99 om uiteindelijk P(0$<$Z$<$a) = 0,495 en a= 2,58 uit te komen.
Echter staat er geen uitleg bij en werd er ook geen uitleg gegeven in de les over deze opgave. Zou u mij kunnen helpen?
Romy
Student universiteit België - dinsdag 16 januari 2018

Antwoord

Hallo Romy,

Eerst maar eens een schets om goed inzicht te krijgen in de vraag. Voor een standaardnormaalverdeling ziet de schets er zo uit:

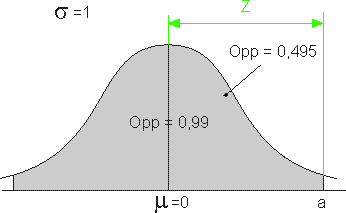
Een Z-waarde geeft aan wat het verschil is tussen een grens (hier: de waarde a) en het gemiddelde, uitgedrukt in een aantal keer de standaardafwijking. Bij de standaardnormaalverdeling is de standaardafwijking 1, dus de afstand van gemiddelde naar a is gelijk aan Z.
De vraag is dus eigenlijk: "welke waarde moeten we kiezen voor a, opdat de oppervlakte onder de kromme tussen $\mu$-a en $\mu$+a gelijk is aan 0,99?" Dan moet de oppervlakte tussen $\mu$ en $\mu$+a gelijk is aan de helft van 0,99. Bij $\mu$ eisen we dus: opp tussen 0 en a is 0,495, ofwel:

P(0$<$Z$<$a) = 0,495

Met behulp van een rekenapparaat of een tabel vinden we: a=2,58.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 18 januari 2018