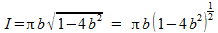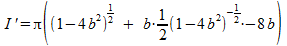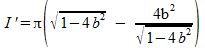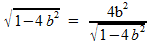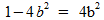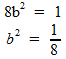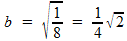WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Maximale inhoud cilinder

Dit is een reactie op vraag 82176

Dag Gilbert,

De afmetingen moeten echter wel kloppen... Ik merk wel dat je de straal en hoogte van de cilinder omwisselt.

Ik kom er zelf niet aan uit. Zal ik je de opgave eens in bijlage sturen?

Dit zijn de stappen die ik heb uitgevoerd:
1) b=x/(x²+1) zodat x=(1+√(1-4b²))/2b of x=(1-√(1-4b²))/2b

2) A ((1-√(1-4b²))/2b , 0) en B ((1+√(1-4b²))/2b , 0) zodat d(A,B)=√(1-4b²)/b

3) Inhoud cilinder bepalen: I(b) = r²$\pi$h = $\pi$b√(1-4b²) , zodat b=√(2)/4

Ik begrijp je redenering dat je er niet van uit mag gaan dat de inhoud maximaal is als de oppervlakte maximaal is, maar waarom kom je bij het berekenen van de maximale oppervlakte alsnog uit op b=0?

Groetjes
Liese
3de graad ASO - vrijdag 13 mei 2016

Antwoord

Hallo Liese,

Je stuurde deze afbeelding op, dat maakt de vraag een stuk duidelijker:

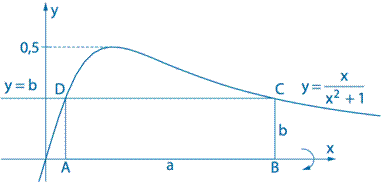
De hoekpunten C en D liggen op de gegeven functie. Nu is de vraag bij welke waarde van b het omwentelingslichaam van de rechthoek ABCD een maximale inhoud heeft.

De x-coördinaten van de punten D en C en daarmee de horizontale zijde a van de rechthoek heb je goed berekend:

a = D(A,B) = √(1-4b²)/b

De inhoud van je cilider klopt ook:

I = $\pi$b√(1-4b²)

Jouw laatste stap is mij echter een raadsel. Om de maximale inhoud te bepalen, berekenen we eerst de afgeleide van I:

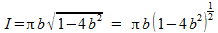
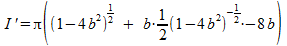
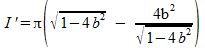
Deze afgeleide gelijkstellen aan nul levert:

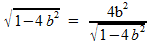
Kruislings vermenigvuldigen:

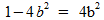
Zodat we uiteindelijk vinden:

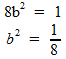
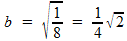
(of -¹/₄√2, maar deze oplossing is voor dit vraagstuk niet relevant).

Nu je b kent, kan je de x-coördinaten van D en C berekenen en de vraag beantwoorden.

OK zo?

Oh ja, jouw laatste vraag over hoe het komt dat je voor het berekenen van de maximale oppervlakte van de rechthoek uitkomt op b=0.
Kijk maar eens naar het plaatje: wanneer je b steeds kleiner maakt, wordt je rechthoek lager maar ook langer. Dit langer worden gaat 'sneller' dan het lager worden. Bij kleiner wordende b blijft de oppervlakte maar groeien en groeien, tot een zekere limietwaarde wanneer b nadert tot 0 en a nadert naar oneindig. Je bereikt nooit een maximale oppervlakte: het maximum zou je pas bereiken bij een oneindig lange en oneindig 'dunne' rechthoek ...

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 14 mei 2016