|
|
|
\require{AMSmath}



Oppervlakteberekening bij bepaalde integratie
Hallo
Bepaal de oppervlakte van de figuur ingesloten door de grafiek van de functie f(x) = x4 - 12x2, de x-as en de verticale lijnen door de buigpunten van de f-grafiek.
Het antwoord is \frac{72}{5}\sqrt{2} maar ik kom daar iets heel anders uit... kan u mij helpen?
Thomas
3de graad ASO - vrijdag 6 april 2012
Antwoord
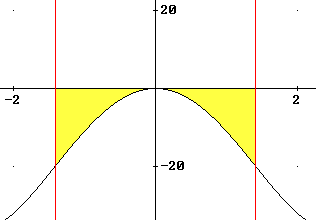
Met x=-\sqrt{2} en x=\sqrt{2} als grenzen krijg je:
Opp. = - \int\limits_{ - \sqrt 2 }^{\sqrt 2 } {x^4 - 12x^2} dx
...en dat moet kunnen...
Anders horen we 't wel.

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 6 april 2012
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2025 WisFaq - versie 3

|











