|
|
|
\require{AMSmath}



Evenwijdige projectie
'Twee evenwijdige lijnstukken hebben dezelfde verhouding als hun beelden bij de evenwijdige projectie.'
Ik moet dit bewijzen door gebruik te maken van volgende stelling: als in een driehoek een rechte evenwijdig is met een zijde, dan verdeelt deze de andere zijden zodat de overeenkomstige lijnstukken evenredig zijn.
peter
Student Hoger Onderwijs BelgiŽ - zaterdag 21 januari 2012
Antwoord
Dag Peter,
Je geeft helaas niet aan wat je al geprobeerd hebt.
Ik geef alleen een plaatje met daarbij een korte toelichting.
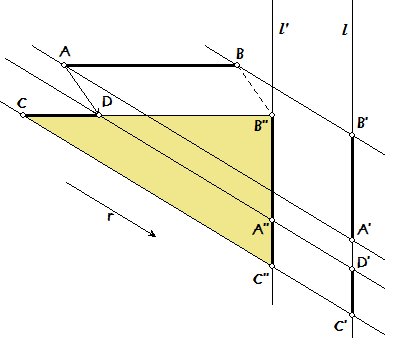
De projecties van de lijnstukken AB en CD op de lijn l zijn A'B' en C'D' (de projectierichting is de richting van de vector r).
Lijnstuk DB" is gelijk aan en evenwijdig met AB (translatie).
De lijn l' gaat door B" en is evenwijdig met l.
Je kan nu bewijzen dat de lijnstukken A"B" en A"C" opvolgend gelijk zijn aan A'B' en C'D'.
Kijk dan naar driehoek B"CC"...
Succes!
DK

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 1 februari 2012
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2025 WisFaq - versie 3
|










