WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Afgeleide (sec x) (1 en tan x)

Dit is een reactie op vraag 65370

Beste Thijs,

Bedankt voor je antwoord.

Dit waren mijn stappen:

f'(x) = ( 1 + tan x)sec(x)tan(x) - sec(x)sec²(x)
----------------------------------------
(1 + tan x)²

f'(x) = sec( tan(x) + tan2(x) - sec2(x) )
---------------------------------
(1 + tan(x))2

f'(x) = sec(x) ( tan x - 1 )
---------------------------------
(1 + tan(x))2

################################################
d
- (tan x) = sec²x
dx

Hoe kom je erbij dat
d
- (tan x) = (1 + tan²x) is.
dx

Nu zie ik dat er bij jou ook het volgende staat:

f'(x) = sec(x)tan(x)(1+tan(x))-sec(x)(1+tan²(x))
----------------------------------------
(1 + tan(x))²

vervolgens ga je naar

f'(x) = sec(x)tan(x) + sec(x)tan²(x)-sec(x) - sec(x)tan²(x)
---------------------------------------------------
(1 + tan(x))²

Het probleem zit hm nog in de teller.
is (1 + tan(x)) gelijk aan sec(x)tan²(x)?

groeten,

Ben
Ben
Student hbo - zaterdag 9 juli 2011

Antwoord

dag Ben,

Goed dat je direct reageert. Nu zie ik ook dat ik je eerste vraag verkeerd gelezen hebt. Je was blijkbaar wel helemaal op de goede weg, je berekeningen klopte ook tot zover, je had het alleen fout genoteerd.

Je vraag was:
Hoe kan sec(tan(x)+tan²(x)-sec²(x)) gelijk zijn aan sec(x)(tan(x)-1)?

Mijn antwoord was dat het niet kan, omdat je het eerste deel fout geformuleerd had.

Het is niet:
sec(tan(x)+tan²(x)-sec²(x))

Maar het moet zijn:
sec(x)*(tan(x)+tan²(x)-sec²(x))

De [sec(x)] moest uit haakjes gehaald worden, niet alleen [sec].
Ik dacht al dat je [tan(x)+tan²(x)-sec²(x)] in de sec(...) verwerkt had, maar dat kan niet de bedoeling zijn geweest.

Als ik je vraag dan nu mag veranderen in:
Hoe kan sec(x)*(tan(x)+tan²(x)-sec²(x)) gelijk zijn aan sec(x)(tan(x)-1)?

Dan zou dit mijn antwoord zijn:

Overigens geldt: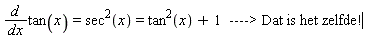

Hopelijk heb ik je nu beter kunnen helpen?

Mvg Thijs Bouten

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 9 juli 2011