WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Enkelvoudige grafen

Weet iemand alle enkelvoudige grafen (tot isomorfie) met valentie rij 2,2,2,3,3,4? of in ieder geval hoeveel het er zijn?

Alvast Bedankt!

Met vriendelijke groeten
Johan
Johan
Student hbo - zondag 25 juli 2010

Antwoord

Dag Johan,

Grafentheorie blijft in mijn ogen toch een tak van de wiskunde waar je zeker kennis nodig hebt, maar waar een groot gedeelte toch bestaat uit puzzelen en logisch beredeneren (hoewel dat ook wel meer takken van de wiskunde zijn).

valentierij 2,2,2,3,3,4.
Er zijn dus 6 punten in deze graaf. geen punt heeft valentie 1, dus er zijn geen zogenaamde 'eindpunten' (punten waar maar één lijn aan verbonden is). Je moet dus in één ronde alle punten kunnen doorlopen (cykel).
valentiesom = 2+2+2+3+3+4=16.
aantal lijnen = valentiesom/2=16/2=8.

Teken 6 punten met daardoor een rondgang. Je hebt nu ook 6 lijnen getekend, de punten hebben allemaal valentie 2. Er moeten dus nog 2 lijnen bijgetekend worden. Deze 2 lijnen moet elkaar ook weer tegenkomen in een zelfde punt (zo krijg je dan een punt met valentie 4). De uiteindes van deze 2 lijnen moeten ieder een ander punt zijn (waardoor je twee punten met valentie 3 krijgt). Houd er rekening mee dat het een enkelvoudige graaf moet zijn (tussen twee willekeurige punten slechts één verbindingslijn).

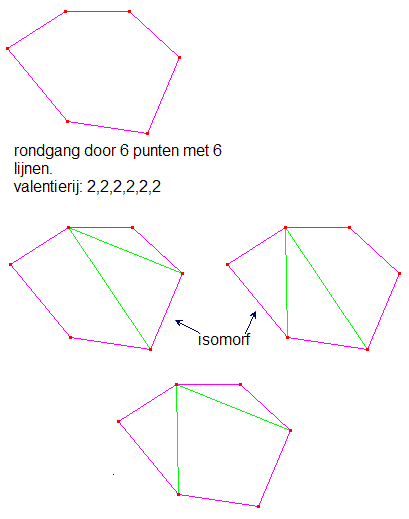
Dit zijn dan twee mogelijkheden... maar er zijn er meer. Zie de reactie en antwoord hieronder.

Met vriendelijke groet,
Thijs Bouten

Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 26 juli 2010

Re: Enkelvoudige grafen