WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

De normale benadering van de binomiale formule

Een hotel in Utrecht heeft 80 kamers. In de zomermaanden is de bezettingsgraad van de kamers ongeveer 75%.
Bereken de kans dat op een zekere dag 50 kamers bezet zijn, gebruikmakend van de normale benadering (benadering met de normale verdeling) van de binomiale verdeling.
Ieder boek of site die ik bekijk staat dat het moet met behulp van de grafische rekenmachine. Die mag ik echter niet gebruiken bij mijn toets. Hoe bereken ik dit dan?

Dankjewel!
Jorien
Student hbo - donderdag 21 januari 2010

Antwoord

Ik ga er vanuit dat hier de kans bedoeld wordt op precies 50 kamers bezet.

X:aantal bezette kamers
X~binomiaal verdeeld met n=80 en p=0,75.
Gevraagd: P(X=50)

Er zijn verschillende manieren om dit oplossen. Ik doe er maar 's een paar.

1.
Met de binomiaalformule:

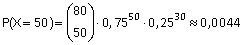
2.
Met de GR of een script (o.i.d.).
3.
Benaderen met de normale verdeling.
Daarvoor bereken je eerst de verwachtingswaarde en de standaarddeviatie.

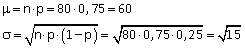
X·:benadering met de normale verdeling van het aantal bezette kamers met bovenstaande $\mu$ en $\sigma$.
P(X=50)=P(49,5$<$X·$<$50,5)
Ik neem nu aan dat je een tabel hebt met de standaard normale verdeling. Bereken de z-scores van 49,5 en 50,5. Bepaal de bijbehorende waarden voor $\phi$(z) en trek de oppervlakten van elkaar af om de kans op X=50 te benaderen.

Zou het dan lukken?

Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 21 januari 2010

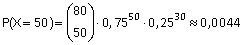
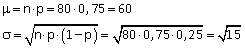
Re: De normale benadering van de binomiale formule