|
|
|
\require{AMSmath}
Parabool, drie rechten en een punt
Een rechte a snijdt een parabool P in twee punten:A en B. Door het midden M van [AB] trekt men de rechte b evenwijdig aan de as van de parabool. Nu gaan de rechte b, de loodlijn l uit brandpunt F (op AB) en dirrectrice d door hetzelfde punt.
Bewijs dit...
Misschien kan iemand me helpen? Ik heb geen idee, ik weet echt niet waar te beginnen!
Evelyn
Evelyn
3de graad ASO - donderdag 11 september 2008
Antwoord
Dag Evelyn,
Sorry voor het wellicht wat lang uitblijven van een antwoord.
Je zou het probleem ook van een iets andere kant kunnen benaderen, namelijk door te bewijzen dat de lijn door het snijpunt (M') van de lijnen b en d en het punt F loodrecht staat op de lijn AB.
In onderstaande figuur staan dan verder nog wat aanwijzingen, om je iets op weg te helpen...
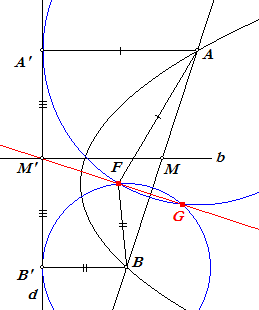
Het punt M' speelt daarbij een belangrijke rol. Zo is M'A' = M'B' (waarom?).
En M'A' en M'B' zijn raaklijnstukken uit M' aan de cirkels (A,AF) en (B,BF); waarom?
Vraag: Gaat de lijn M'F ook door het tweede snijpunt G van die cirkels?
Als je die vraag ook hebt beantoord, dan is het niet moeilijk meer om in te zien dat M'F inderdaad loodrecht staat op AB.
Succes!
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 15 september 2008
|
|
home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|
Re: Parabool, drie rechten en een punt