WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Twee-factor variantie-analyse

Hey!

Ik zit wat in de problemen met de twee-factor ANOVA...
1) Wat zijn de voordelen van een twee-factor ANOVA tov een één-factor ANOVA? En waarop moet je letten (vb. gegevens) bij het beslissen van het gebruik van één-factor of twee-factor ANOVA?
2) We zijn een tijdje beziggeweest met hoofdeffecten en interactieeffecten die je "duidelijk" kan zien op grafieken, maar als ik een grafiek bekijk lijkt het alsof ik in het oneindige zit te staren. Waaraan kun je duidelijk zien of er een hoofdeffect en/of interactieeffect is, bvb een grafiek met een "kruis", of een grafiek met 2 "parallelle lijnen",... wat zijn de kenmerken dat je over een hoofd- of interactieeffect kunt spreken? En waarop moet je letten voor de interpretatie, want ik denk dat het niet om "zomaar" een interactieeffect is, maar interactieeffect tussen 2 factoren?

Ik hoop dat jullie me kunnen helpen, nog een fijne maandag!

Groetjes,

Sandra
Sandra
Student Hoger Onderwijs België - maandag 14 mei 2007

Antwoord

Dag Sandra,

Ik ben geen specialist. Maar deze vraag staat nou al een hele tijd. Dus zal ik toch maar proberen je op weg te helpen.

Eerst maar vraag 2). Ik mij zitten afvragen watvoor grafieken je bedoelt. Waarschijnlijk is het dit. Zeg even dat X_ij de afhankelijke variabele is met i en j de twee onafhankelijke. Dan bedoel je waarschijnlijk dat voor verschillende waarden van i een grafiek van X_ij is gemaakt, met j op de horizontale as. Inderdaad kun je de interactie uit die grafieken aflezen. Als er geen interactie is lopen de grafieken evenwijdig. Bv: X_1j = a₁ + b_j en X_2j = a₂ + b_j = X_1j - a₁ + a₂. (de ruis niet meegerekend). Als de grafieken niet evenwijdig lopen of elkaar kruisen dan heeft j voor i=1 een ander effect op X_ij als voor i=2. Dan is er dus interactie.

Dan vraag 1) In het algemeen is het voordeel van het gebruiken van twee factoren dat je populaties makkelijker kunt scheiden. Ik had daar een mooi plaatje bij gemaakt:

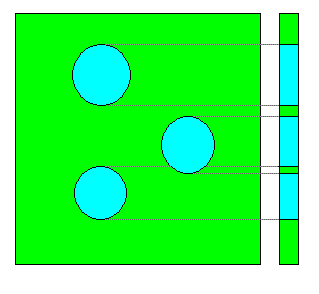
De drie vlekken in de rechter driehoek zijn drie populaties. De punten zijn geplot met een variabele op de horizontale as en een andere op de vertikale as. Ze zijn duidelijk van elkaar te onderscheiden. Op de rechter balk zie je wat er gebeurt als je alleen de vertikale as gebruikt. De onderste twee populaties overlappen en de bovenste zit er heel dichtbij.

Maar bij ANOVA zit het anders. Je hebt de populaties al, en je wilt onderzoeken of de gemiddelden X_i. van elkaar verschillen. En idem voor de X_.j.

Als X sterk van twee variabelen afhangt is het nadeel van 1-factor anova met één van de variabelen dat er kunstmatig grotere ruis (SST) ontstaat door de variaties van de tweede variabele.

Een complicatie van 2-factor anova is natuurlijk de interactie. Als je n i's hebt en m j's krijg je niet alleen n+m gemiddelden, maar ook nog eens n*m interactietermen.

Dit is zeker niet het hele verhaal. Maar misschien heb je er wat aan. Hieronder nog een link die de voordelen opsomt, maar niet al te helder. Laat eens horen wat jij er in ziet. Misschien komen we dan verder.

Groet. Oscar

Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 22 mei 2007