WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Binomiaalverdeling 2

Alvast bedankt voor het snelle antwoorden! De methode met het rekenmachine is heel handig om te controleren maar op het examen is het de bedoeling om het handmatig te doen met de tabel en de formule: (n boven k) p^k(1-p)^n-k
Hoe kan ik deze oefening dan oplossen met behulp van de formule en de tabel? Hoe kom ik aan die k en hoe moet ik de (n boven k)uitrekenen?
Stel dat X een binomiaal verdeelde toevalsvariabele is. Bepaal dan:
P(X=2) n=8, p =0.20
P(X7) n=13,p =1/3
P(X2) n=5, p=0.60

Nogmaals bedankt!
Eline
Student universiteit België - zondag 28 januari 2007

Antwoord

Binomiaal verdeelde kansen van de vorm P(X=...) kan je uitrekenen met de formule.
Zie Uitleg formule en 't voorbeeld...

Kansen van de vorm P(X...) of P(X...) kan je bepalen met behulp van een tabel. Bij je tweede voorbeeld: zoek de tabel voor n=13 en in de kolom p=¹/₃ kan je de cumulatieve kansen vinden.

Ik neem aan dat je zo'n tabel hebt...

Bij het derde voorbeeld kan je 't ook nog wel uitrekenen... mag je wel een 'gewone' rekenmachine gebruiken? Zo niet... dan moet je nog even kijken op 3. Faculteiten, permutaties en combinaties. Het kan dus met faculteiten, maar het kan handiger:

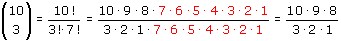
Als je dat gewend bent gaat het nog best. Lukt dat zo?

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 28 januari 2007