WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Vierhoek

Willekeurige vierhoek, plaats de kwadraten op de zijden, bepaal de middelpunten van, verbind tegenovergestelde middelpunten, bewijs dat die lijnen zich steeds kruisen onder een rechte hoek...
dujard
Ouder - maandag 23 oktober 2006

Antwoord

Hallo,

We beginnen met een hulpstelling:
Laten we twee vierkanten ABCD en AEFG bekijken met een gemeenschappelijk punt A. Dan bewijzen we dat de middelpunten M en K van die vierkanten tezamen met de middens N van DE en L van BG weer een vierkant vormen.

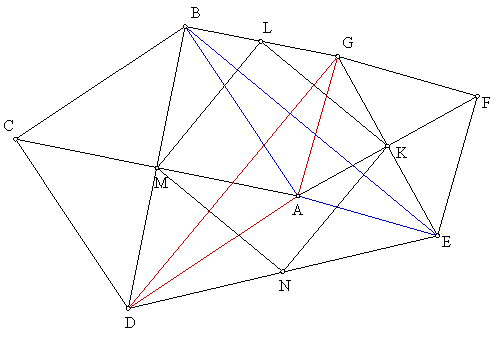
We kunnen dit als volgt zien:

Merk op dat driehoeken ABE en ADG in elkaar overgaan bij rotatie over 90° dan wel -90° om A. Zij zijn dus congruent, in het bijzonder geldt BE = DG en BE^DG.

Nu is KN een middenparallel in driehoek EDG en LM in BGD. Deze twee lijnstukken zijn dus evenwijdig met DG en half zo lang.

Net zo zijn KL en MN evenwijdig met BE en half zo lang.

Dus KLMN is een vierkant.

Gaan we nu naar jouw probleem, dan hebben we de volgende figuur:

Laat S het midden van BD zijn. Dan geldt met bovenstaande hulpstelling dat SM en SP zijden zijn van een vierkant, en dus even lang en loodrecht op elkaar. En hetzelfde geldt voor SO en SN.

Maar dan zijn de driehoeken OSM en NSP beelden van elkaar bij rotatie over ±90° om S. En dat betekent dat MO en NP loodrecht op elkaar staan, zoals gevraagd.

****

Nog even iets over de hulpstelling waarmee we begonnen. Eigenlijk is het een bijzonder geval van een veel algemenere stelling.

We maken gebruik van de Stelling van Miquel. De betekenis van die Stelling is veel groter dan alleen het door één punt gaan van drie cirkels. Dat is prima uitgelegd in de Stelling van Miquel van Dick Klingens, met name Stellingen 3a en 3c aldaar.

Een korte samenvatting, met de volgende figuur:

We zijn begonnen met een driehoek A₁B₁C₁ die in een driehoek ABC is "ingeschreven". Met Miquel's stelling weten we dat de getekende cirkels door een punt P gaan. Het aardige is ook dat we weten dat hoeken PA₁B en PC₁B samen 180 graden zijn (algemeen in een koordenvierhoek). En natuurlijk ook hoeken PC₁B en PC₁A. Dus hoeken PA₁B en PC₁A zijn gelijk. En natuurlijk op dezelfde manier is PB₁C ook gelijk aan deze twee.

Laten we nu A'B'C' de voetpuntdriehoek van P zijn (dus de verbindingslijntjes PA', PB'en PC' staan loodrecht op de zijden). Dan zijn de driehoeken PA₁A', PB₁B' en PC₁C' gelijkvormig. Bovendien zijn A₁B₁C₁ en A'B'C' gelijkvormig (Stelling 3c). Het is zelfs sterker: alle driehoeken ingeschreven in ABC die gelijkvormig aan A'B'C' zijn, hebben hetzelfde punt P als Miquel punt.

Nou is er iets aardigs: als we twee gelijkvormige driehoeken A₁B₁C₁ en A₂B₂C₂ hebben, dan hebben die dus hetzelfde Miquel punt P. Dan zijn de driehoeken PA₁A₂, PB₁B₂ en PC₁C₂ dus gelijkvormig. We nemen nu de middelpunten M_A van A₁A₂, M_B van B₁B₂ en M_C van C₁C₂. De driehoeken PM_AA', PM_BB' en PM_CC' zijn dan ook gelijkvormig. Maar daaruit leiden we weer af dat M_AM_BM_C het punt P als Miquel punt heeft, en dat M_AM_BM_C ook aan de gegeven twee driehoeken gelijkvormig is.
Duidelijk is ook dat we voor M_A ten opzichte van A₁A₂ een andere verhouding in plaats van het midden kunnen nemen als we maar voor M_B en M_C dezelfde verhouding nemen.

Wat heeft dit alles met de hulpstelling te maken?

Wel. Stel we hebben twee vierkanten A₁A₂A₃A₄ en B₁B₂B₃B₄. Dan vormen de middens M_i van A_iB_i voor i=1,2,3,4 volgens het bovenstaande weer een vierkant. We concluderen immers dat M₁M₂M₃ een rechthoekige gelijkbenige driehoek is net als A₁A₂A₃ en B₁B₂B₃. Net zo met M₂M₃M₄. En zo hebben we het vierkant M₁M₂M₃M₄.

De hulpstelling is hier een bijzonder geval van.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 25 oktober 2006