WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Standaardnormale verdeling (tabel)

Ik heb moeite met volgende opgave:

Een labo bepaalt in een visstaal Hg via een methode op basis van AAS. In werkelijkheid bevat het staal (gemiddeld) 1,80 ppm. De meetmethode is echter niet perfect, zoals aangegeven door een standaarddeviatie van 0,10 ppm. Wat is de kans dat de laborant die het staal onderzoekt, een ùeetresultaat van 2,00 ppm of meer vaststelt?

Ik deed het volgende:
P(X2) = P( (X- µ)/s (2-1,8)/0,1 ) = P ( Z 2)
dit zouden we dan uit de tabel moeten kunnen afleiden en het zou 2,28% moeten uitkomen maar ik begrijp niet goed hoe ik met die tabel moet omspringen ?
Een kleine schets van de (door u wellicht gekende) tabel:*
van linksboven naar rechts: x | 9 8 7 6 5 4 .... 0
van linksboven naar onder
x
-3,9
-3,8
-3,6
.
.
.
+3,9

Zou iemand het me kunnen duidelijk maken aub?

Alvast hartelijk dank bij voorbaat!

mvg

Hilde
Student universiteit België - woensdag 26 juli 2006

Antwoord

Ja hoor... eigenlijk staat het wel bij zo'n tabel...

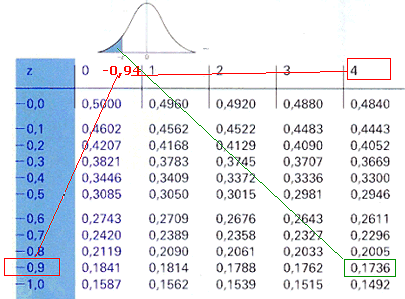
Hier lees ik af dat bij z=-0,94 hoort een oppervlakte van 0,1736, oftewel:
F(-0,94)=0,1736

Dus P(X-0,94)=0,1736

Lukt dat zo?

Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 26 juli 2006

Re: Standaardnormale verdeling (tabel)