WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Ellips-bewijs

Geachte wiskundigen,
Beetje beleefd, maar ja mijn probleem is dan heel dringend, ik moet nog namelijk 1 oefening maken voor mijn eindwerk en heb er al talloze bomen doorgejaagd, het probleem is simpel eigenlijk, ik weet gewoon niet waar te beginnen.

De opgave: men neemt op de ellips E: x²/a² + y²/b² = 1 een veranderlijk punt D. Men trekt de raaklijn t en de normaal n in D aan E. We noemen P de loodrechte projectie van O op t en N het snijpunt van n en de grote as. Bewijs dat de afstand van OP maal de afstand van DN constant is.

Ik heb al dingen geprobeerd zoals de afstandformule gebruiken maar dan komt men iets uit met vierkantswortels en allerlei coordinaten van de punten. Dus enige hulp zou enorm welkom zijn, alvast bedankt!
Steven
3de graad ASO - zondag 26 maart 2006

Antwoord

Dag Steven,
Soms is het handiger om niet direct naar analytische methoden te grijpen ('t scheelt bomen)...
Zo ook hier. 'Gewone' meetkunde wil soms ook wel.
Kijk eens naar het onderstaand plaatje, waarin het punt D de coördinaten (x₀,y₀) heeft, D' de projectie is van D op de x-as en T het snijpunt van t met de y-as.

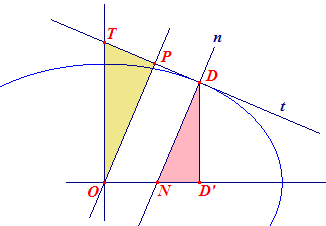
Ik geef enkele aanwijzingen, waarmee je, denk ik, wel verder kan.
Je hoeft mijns inziens alleen van de vergelijking van de rechte t (de raaklijn) gebruik te maken.

(1) Hoe groot is DD'?
(2) Toon aan dat OT = b²/y₀
(3) Waarom zijn de driehoeken D'DN en POT gelijkvormig?
(4) Wat weet je dan van de verhoudingen DN : OT en DD' : OP?
(5) Laat zien dat de bedoelde constante gelijk is aan b².

En verder: succes met je eindwerk.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 26 maart 2006