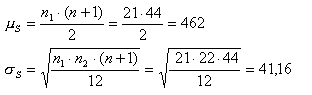WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Mann Whitney

Hallo,

Voor een opdracht van mijn opleiding ben ik bezig met verschillende hypothese toetsen.
Nu wil ik ook de Mann Whitney toets doen. Echter kom ikhier op een probleem. Ik kan namelijk nergens vinden hoe ik het kritieke gebied kan berekenen bij 43 rangnummers.De afgelopen week ben ik continue met kans2 bezig geweest. Ik heb bij mijn cijfermateriaal de volgende toetsen uitgevoerd: De T-toets en de F-toets daarnaast ben ik bezig met Mann Whitney. Hier kom ik echter op een probleem, in de reader die ik van Kans 2 heb staat het totaal aantal rangnummers tot 20. Echter heb ik 43 rangnummers. Nu kan ik in de reader nergens vinden hoe ik hierbij het kritieke gebied moet berekenen. Ik heb alles tot het punt waar ik dat gebied moet uitrekenen.
Weten jullie misschien hoe het moet?

Even een paar extra gegevens:
Met een kritiekgebied van á= 0,05. De toets is tweezijdig.
De som van alle rangnummers is gelijk aan , waarbij n = n1+n2 In dit geval is n1 het aantal leerlingen van klas 1G, dat zijn er 21 en is n2 het aantal leerlingen van klas 1H en dat zijn 22 leerlingen.

n = 21 + 22 = 43

Omdat ik de rangnummers van klas 1G bij elkaar op moet tellen gebruik ik Excel om de tabel te sorteren op klas.
Zoals je in de rechter tabel kan zien.
De som van alle rangnummers van klas 1G is: 462
De som van de rangnummers van klas 1H is: 484.
Ter controle 462 + 484 = 946 en dit klopt met de formule die ik eerder heb toegepast

De tabel met de gegevens hoe ik die nu heb:
Klas Cijfer Rangnummer
1G 28 1
1H 38 2,5
1H 38 2,5
1G 39 4
1H 40 5
1H 44 6
1G 45 7
1G 51 8
1G 54 9
1G 58 10,5
1G 58 10,5
1H 60 12,5
1H 60 12,5
1H 61 14
1G 64 15
1G 65 17
1G 65 17
1H 65 17
1H 66 19,5
1H 66 19,5
1H 68 21,5
1H 68 21,5
1H 70 23,5
1H 70 23,5
1G 71 25,5
1G 71 25,5
1G 74 27
1G 75 29
1G 75 29
1H 75 29
1G 78 31,5
1H 78 31,5
1G 79 33,5
1H 79 33,5
1H 83 36
1H 83 36
1H 83 36
1G 85 38
1H 89 39
1G 94 40,5
1G 94 40,5
1H 95 42
1G 99 43

Als jullie mij hiermee kunnen helpen ben ik heel blij.
Op mijn pc heb ik in excel de software Analyse-it, helaas kom ik hiermee niet verder dan wat ik handmatig heb gedaan.
Alvast bedankt!
Groetjes Heidi
Heidi
Student hbo - woensdag 8 maart 2006

Antwoord

Hoi Heidi,

Twee zaken die hier een rol spelen
1) De tabel gaat maar tot een totaal van 20 metingen (boven dit aantal moet je een normale benadering gaan toepassen)
2) De gegevens bevatten knopen (ties). Hierop kan je in de berekening corrigeren.
Ik vraag me echter af of je dat op HBO niveau moet doen. De meeste boeken vermelden deze correctie niet!!. Je zou aan je docent eens moeten vragen of hij/zij verwacht dat je bij deze toets een knopencorrectie moet uitvoeren. Waarschijnlijk weet je docent dan zelf niet waar je het over hebt

Hoe los je dat nu op (zonder knopencorrectie)?
Neem voor het gemak aan dat n₁ het aantal is van de kleinste steekproef dus die 21 in klas G. Dat is in ieder geval groter dan 10 waardoor ik een normale benadering zonder meer mag toepassen.
zij nu S de som van de rangnummers in de steekproef van die klas G. Dan is S normaal verdeeld met:

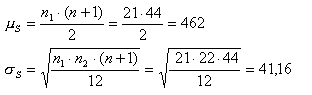
Bij het toetsen (a=0,05) van de nulhypothese (geen verschil tussen de groepen) zijn de grenzen van het kritiek gebied m_S±z·s_S = 462 ± 1,96 · 41,16. Dat levert een linkergrens op van 381,3 en een rechtergrens van 542,7. Blijf je hiertussen met je toetsingsgrootheid S dan is er geen aantoonbaar verschil tussen de totale groepen.
Die toetsingsgrootheid S had je zelf al berekend: som van alle rangnummers van klas 1G is 462. En dat betekent dan uiteraard geen verschil.

Opm. die 462 die uit de opgetelde rangnummers komt is toevallig gelijk aan die 462 bij m_S. Normaal zal dat niet het geval zijn. Dat betekent dat deze opgave erg flauw is (je komt met de S precies op de m_S uit) zodat je eigenlijk niet eens zou hoeven te toetsen. Daarnaast is het feit dat er twee keer 462 uitkomt verwarrend en absoluut niet slim gekozen als opdracht. Maar dat even terzijde.

Daarnaast is de vraag of je wel terecht gaat toetsen. Toetsen doe je als je op basis van twee steekproeven uit grotere populaties iets wil zeggen over eventuele verschillen in de populaties. Maar hier vergelijk je twee complete klassen G en H en zijn dat dus al de hele populaties. Waarom toets je dan ???? Ik weet het eigenlijk niet.... maar misschien zit daar wel een diepere gedachte achter. Nog een leuk vraagje voor je docent dus

Hopelijk is alles duidelijk.
Met vriendelijke groet

JaDeX

Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 9 maart 2006