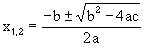WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Vierkantsvergelijking

hallo, ik zit in de problemen, kan iemand mij helpen met dit:
Als ca0 en als a-b+c=0, zoek dan de grootste oplossing van ax²+bx+c=0
thomas
2de graad ASO - woensdag 14 september 2005

Antwoord

Beste

De oplossing van een kwadratische vergelijking vind je met de abc-formule. De abc-formule is een formule waar juist voor de wortel ± staat. Is het nu de + of de - die zorgt voor de grootste oplossing?

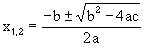
Omdat de noemer in de formule, a, positief is, is de oplossing het grootst als de teller maximaal is. De teller is het grootst als er voor de wortel een + staat. We kiezen dus voor de plus!

Nu is de oefening nog niet af. Je kan de abc-formule met het plus teken nog verder vereenvoudigen gebruikmakende van de gegevens, immers:

D = b²-4ac = (a+c)²-4ac=a²+c²+2ac-4ac = a²+c²-2ac = (a-c)²

Let wel op het absolutewaarde-teken, dat is nodig omdat ca (gegeven):

ÖD = |a-c| = c-a

Nu kan je het laatste beetje wel zelf zeker?
Groetjes

Igor

Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 14 september 2005