WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Betreffende niet-Euclidische meetkunde

Dit is een reactie op vraag 38098

Ik heb eerder gevraagd hoe je een lijn in een pioncareschijf kunt construeren. Daarna vroeg ik het bewijs van die constructie. En werd mij verteld dat er niet van een bewijs kan worden gesproken, omdat het alleen maar gaat over een cirkelboog die loodrecht op de horizon staat. Dat wist ik ook wel, maar hoe bewijs je dat die constructie klopt en dat je wel degelijk een cirkelboog hebt die er loodrecht opstaat?

Vriendelijk bedankt,

Marten
Leerling bovenbouw havo-vwo - dinsdag 17 mei 2005

Antwoord

De vraag is dus:
hoe construeer je een cirkel (M) door twee gegeven punten A en B, beide gelegen binnen een cirkel (O), en wel zo, dat de cirkel (M) de cirkel (O) loodrecht snijdt.
En, bewijs de juistheid van de constructie.

We bekijken de volgende stappen.
Stap 1.
In onderstaande figuur gaan we uit van een cirkel (O) en een daarbinnen gelegen punt A.

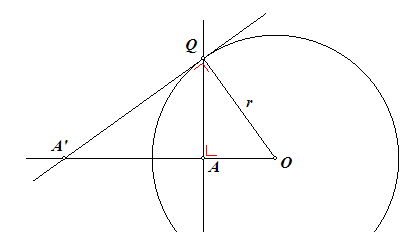
De lijn AQ staat loodrecht op de lijn OA en de lijn QA' staat loodrecht op de lijn OQ met |OQ| = r.
Dan is:
OA · OA' = r²
Bewijs:
Bekijk de driehoeken OQA' en OAQ. Deze zijn gelijkvormig.
Dan is:
OA' : OQ = OQ : OA, zodat OQ² = r² = OA · OA'

Nb. Het punt A' heet het inverse punt van A tov. de cirkel (O).

Stap 2.
We gaan in onderstaande figuur weer uit van een punt A met het daarbij volgens stap 1 geconstrueerde punt A'.

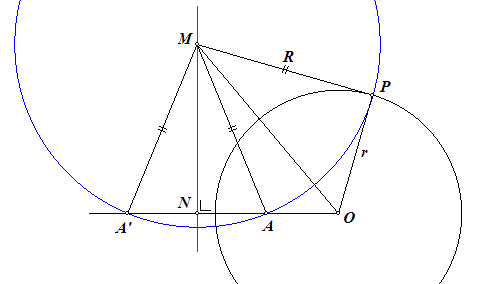
We kiezen het punt M op de middelloodlijn van AA'; N is het midden van AA', met |NA| = p en |MA| = R.
De cirkel (M) snijdt (O) in een punt P, zodat ook |MP| = R.
Dan is hoek MPO = 90° (maw. de cirkels snijden elkaar loodrecht).
Bewijs:
OA · OA' = OA · (OA + 2p) = OA² + 2p · OA + p² - p² = (OA + p)² - p² = ON² - p²
dus:
OA · OA' = ON² - (R² - MN²) = ON² + MN² - R² = OM² - R²

Samen met hetgeen gevonden is in stap 1, geeft dit:
OM² - R² = r², of:
OM² = R² + r²
En dan is hoek MPO = 90° (omgekeerde stelling van Pythagoras).

Stap 3.
In onderstaande figuur hebben we nu de punten A, A' (inverse van A) en B, B' (inverse van B).

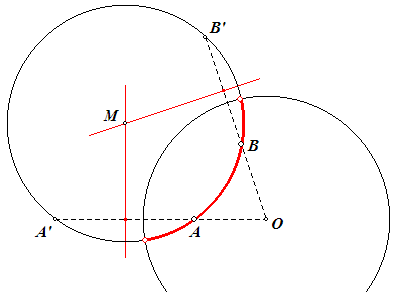
De middelloodlijnen van AA' en BB' snijden elkaar in een punt M.
De cirkel met middelpunt M die door A en B gaat, snijdt de cirkel (O) dus loodrecht.

Met andere woorden:
de boog van die cirkel die binnen de cirkel (O) ligt, is een zogenoemde d-lijn in de Poincaré-disk (een lijn door de punten A en B), bepaald door de cirkel (O).
Zie Het Poincaré-model van de hyperbolische meetkunde

Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 18 mei 2005