WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Bewijs zwaartelijnen in willekeurige driehoek

Kunnen jullie het bewijs van de zwaartelijnen in een willekeurige driehoek online zetten?

ellyne
2de graad ASO - woensdag 23 maart 2005

Antwoord

Het bewijs dat de zwaartelijnen door hetzelfde punt gaan met behulp van coördinaten?
On-line? Maar natuurlijk niet het 'gehele' bewijs.
Het kan als volgt.

Kies een 'handig' assenstelsel; dat mag in de analytische meetkunde.
Zie de figuur hieronder (O is het midden van AB).

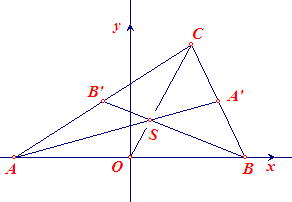
Dan
A = (-a, 0), B = (a, 0), C = (p, q)
Voor het midden A' van BC geldt dan:
A' = ( ¹/₂(p+a), ¹/₂q )
Voor het midden B' van AC geldt:
B' = ( ¹/₂(p-a), ¹/₂q)
De lijn AA' heeft dan als vergelijking:
y = (¹/₂q)/(¹/₂(p+a) + a)·(x + a) = q/(p - 3a)·(x + a)
en de lijn BB':
y = (¹/₂q)/(¹/₂(p-a) - a)·(x - a) = q/(p-3a)·(x - a)

Controleer zelf de juistheid van beide laatste vergelijkingen!

Als je dan het snijpunt S van AA' en BB' uitrekent (dat vraagt wel wat rekenwerk), moet je vinden:
S = (1/3·p, 1/3·q)
En dat punt ligt op CO (en dat is de derde zwaartelijn).
Waarom is dat eigenlijk zo?

Het kan misschien ietsje handiger als je ook nog handige ijk kiest.
Bijvoorbeeld die, waarbij A = (-2,0) en B = (2,0).

Voor enkele bewijzen met 'gewone' meetkunde zie onderstaande link.

Zie Zwaartelijnen in een driehoek

Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 24 maart 2005