|
|
|
\require{AMSmath}
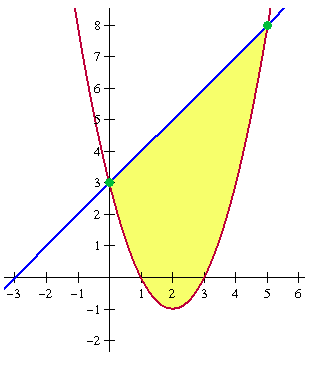
Oppervlakte van functies
Hoe bereken ik de positieve oppervlakte van deze figuur? Alvast bedankt voor jullie hulp, misschien kan ik voor mijn wiskunde er geraken dit jaar...
f(x) = x2 - 4x + 3
g(x) = x + 3
steven
Student Hoger Onderwijs België - woensdag 5 juni 2002
Antwoord
De snijpunten liggen in (0,3) en (5,8).
De oppervlakte tussen twee krommen is altijd gelijk aan de integraal van 'bovenste functie' minus 'onderste functie'.
De ligging t.o.v. de x-as is hierop niet van invloed!
$
\eqalign{
& \int\limits_0^5 {g(x) - f(x)\,\,dx} = \cr
& \int\limits_0^5 {x + 3 - (x^2 - 4x + 3)\,\,dx} = \cr
& \int\limits_0^5 { - x^2 + 5x\,\,dx} = \cr
& \left[ { - \frac{1}
{3}x^3 + 2\frac{1}
{3}x^2 } \right]_0^5 = \cr
& 20\frac{5}
{6} - 0 = \cr
& 20\frac{5}
{6} \cr}
$
MBL
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 5 juni 2002
|
|
home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2025 WisFaq - versie 3
|
