WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Zwaartelijnen

Dit vond ik op een site:

In driehoek ABC zijn D en E de middens van AB en AC.
Trek nu CG // AB en verleng ED tot G.
Nu is in de driehoeken ADE, CDG:
(1) A = C (Z-hoeken)
(2) AD = CD
(3) D = D (overstaande hoeken)
Dus ADE, CDG zijn congruent (HZH), waaruit volgt dat CG = AE = EB ......(4)
en
ED = DG = ¹/₂EG ......(5)
Nu is BCGE een parallellogram, waaruit volgt dat EG // BC, en dus ook ED // BC.
Maar ook BC = EG, zodat uit (5) volgt: ED = ¹/₂BC ¨

Die op een na laatste zin "Nu is BCGE een parallellogram", klopt dat???
Want volgens mij kun je dat niet zo zeggen. Wilt u mij het correcte antwoord toesturen. Bedankt!
Michae
Leerling bovenbouw havo-vwo - dinsdag 8 maart 2005

Antwoord

Jammer dat je niet aangeeft WAAROM je, volgens jou, dat niet zo kunt zeggen.

Het bovenstaand bewijs is evenwel juist (voor bedoelde website zie de link).
De gebruikte figuur op die site staat hieronder.

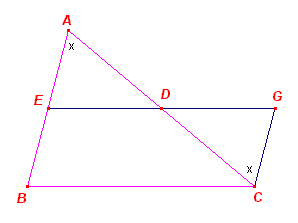
De lijn CG is evenwijdig (getrokken) met AB, dus CG // EB.
En ook, blijkens (4): CG = EB.
En dan is BCGE inderdaad een parallellogram.

Het is niet zo moeilijk te bewijzen dat (Stelling:) als twee zijden van een vierhoek evenwijdig én gelijk zijn, ook het tweede stel zijden daarvan evenwijdig is.
Met andere woorden, deze Stelling is gelijkwaardig met de definitie van parallellogram (een vierhoek met twee paar evenwijdige zijden).

Zie Concurrentie van zwaartelijnen in een driehoek

Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 8 maart 2005