WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Ruit

Kunt u bewijzen dat de oppervlakte van een ruit gelijk is aan de hoogte maal de lengte van een zijde?
En kunt u bewijzen dat alle zijden van een ruit de zelfde lengte hebben?
Piet
Leerling bovenbouw havo-vwo - dinsdag 8 februari 2005

Antwoord

Beide vragen kan ik inderdaad met 'ja' beantwoorden.

Als bewijs daarvan eerst maar eens de oppervlakte.
Kijk naar onderstaande figuur.

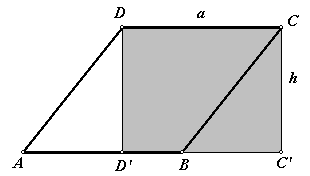
Daarin is:
CD = a; CC'^AB en DD'^AB. En verder is h de hoogte van de ruit, een loodlijn uit een hoekpunt op een 'overstaande zijde'. Dan is:
Opp(AD'D) = Opp(BC'C) ... waarom?
Dus Opp(ABCD) = Opp(D'C'CD) ... d'r gaat wat af en d'r komt hetzelfde bij; en we krijgen een rechthoek.
En dan is:
Opp(D'C'CD) = h·a

En wat je tweede vraag betreft.
Meestal wordt de volgende definitie van ruit gebruikt:
Een ruit is een parallellogram waarvan twee 'opvolgende' zijden gelijk zijn.
En dan valt er echt 'niets' c.q. 'niet veel' te bewijzen (als je weet wat een parallellogram is) .

Als je uitgaat van:
Een ruit is een parallellogram waarvan de diagonalen loodrecht op elkaar staan
dan kan je eenvoudig, met behulp van twee congruente, rechthoekige driehoeken, bewijzen, dat alle zijden gelijk zijn (maak daartoe zelf een tekening van een parallellogram met loodrechte diagonalen).

En kijk eventueel op de webpagina via onderstaande link.

Zie Over vierhoeken

Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 9 februari 2005