WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Pokeren

Er is een vraag die ik niet snap, namelijk de volgende:
Je moet bij pokeren om een flush te hebben, 5 kaarten hebben van dezelfde soort, dus bv. harten. Dan is het experiment: Trek aselect en zonder terugleggen 5 kaarten uit een volledig kaartspel, waarbij de stochast X is, dus bij 2 harten is de stochast X=2

b) Stel de kansverdeling van X op. Hier snap ik het al niet meer, ik doe namelijk de volgende berekeningen: (bij x=2)

5¸52´4¸51´49¸50´48¸49´47¸48´´ 5 boven 2 (ik weet het teken ervoor niet meer)
En hier gaat het dus fout want mijn antwoord is dan
0,07088989442 terwijl het 0,2743 moet zijn...Maar bij een andere opdracht was dit wel de goede methode dus ik snap het niet meer...

c) Hoe groot is de kans om bij een spelltjes poker in de eerste ronde meteen een flush harten van de bankhouder te krijgen?

d) Bij hetzelfde kansexperiment is de stochast Y het aantal azen in de trekking. Stel de kansverdeling van Y op.

e) Hoe groot is de kans dat je in de eerste ronde van een spel poker meteen 4 azen van de bankhouder krijgt?

wie o wie helpt me?
alvast bedankt!!!

Moderne wiskunde vwo bovenbouw A1-2 B1-2 S5 opgave 12
Alexan
Leerling bovenbouw havo-vwo - zondag 6 februari 2005

Antwoord

Bij b. vlieg je de bocht uit. Er zijn 13 harten en 39 niet-harten, dus P(X=2) zal dan toch wel zoiets moeten worden:

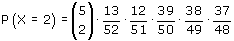
..en waarom is dat een goede methode? Wel aan, eerst bereken je de kans op 2 harten en 3 niet-harten... precies in die volgorde... en dat vermenigvuldig je met het aantal volgordes dat je kan maken. De 5 boven 2....

De rest gaat precies zo... probeer maar!

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 6 februari 2005

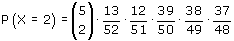
Re: Pokeren