WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Stelling van Desargues

Dit is een reactie op vraag 33221

Ik snap nog steeds niet wat er gebeurt dan...waaarom AQ en BP, Waarom AA' en BB' enz...
TH
Leerling bovenbouw havo-vwo - dinsdag 25 januari 2005

Antwoord

We geven hieronder het bewijs (iets uitvoeriger dan op de eerder vermelde website, en onafhankelijk ervan) van de 'omgekeerde' stelling van Desargues:
Als de driehoeken ABC en A'B'C' lijnperspectief zijn, dan zijn ze ook puntperspectief.
Bekijk de figuur.

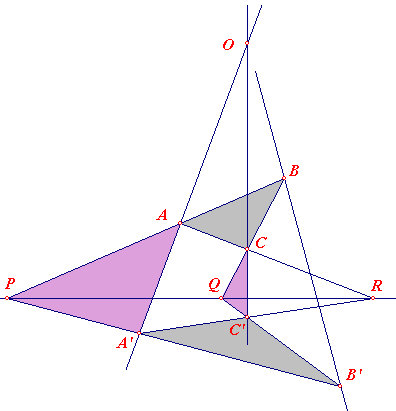
Lijnperspectief wil zeggen (/\ betekent 'snijpunt'):
AB /\ A'B' = P, BC /\ B'C' = Q, CA /\ C'A' = R
liggen op één lijn.
We weten dus: P, Q, R op één lijn.
En dan moeten we bewijzen, dat de lijnen AA', BB', CC' door één punt gaan (om de driehoeken puntperspectief te laten zijn).

Stel de lijnen AA' en CC' snijden elkaar in O.

Dan moet de derde lijn, en dat is BB', ook door O gaan, of anders gezegd: O moet op BB' liggen.
Dat willen we dus bewijzen.

Bekijk nu het punt R samen met de driehoeken APA' en CQC'.
Duidelijk is dat deze driehoeken puntperspectief zijn via het punt R, immers de lijnen AC, PQ, en A'C' gaan door R.
Bekijken we nu de snijpunten van de 'overeenkomstige' zijden van beide driehoeken:
AP en CQ hebben snijpunt B
PA' en QC' hebben snijpunt B'
AA' en CC' hebben snijpunt O
Volgens de ('echte') Stelling van Desargues geldt dan: O, B, B' liggen op een lijn.
En dat wilden we bewijzen.

Ik hoop dat het nu wat duidelijker is.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 25 januari 2005