WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Stelsel ongelijkheden

Hallo Wisfaq,
A.los volgend stelsel op:(grafisch en algebraisch)
2x-3y-15 /stelse(1)
-x+3y12
x+50
-y0
B. Bepaal op grafische wijze het punt dat voldoet aan stelse (1)waarvoor z=-y+x minimaal is en bereken nauwkeurig de coordinaten van dat punt,alsook de er mede overeeenstemmende minimale waarde van z.
C.Bereken de oppervlakte van de doorsnede(gemeenschappelijk dee) van de oplossiingenverzameling van het stelsel (1) met de verzameling punten die voldoen aan de ongelijkheid xy0.
Een hele boterham ....
Graag jullie hulp!
Groeten van Hendrik
hl
Ouder - zaterdag 18 december 2004

Antwoord

A: In onderstaande grafiek voldoen de punten in het "witte" gebied aan het stelsel.

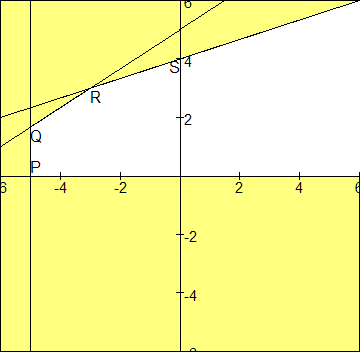
Je kunt dit zelf bepalen door de lijnen 2x-3y=-15, -x+3y=12, x=-5 en y=0 te tekenen en aan te geven welke punten niet voldoen aan de respectievelijke ongelijkheden. Je houdt dan vanzelf de punten over die wel voldoen.
Als je het helemaal mooi wilt doen bereken je ook nog even de hoekpunten P, Q en R.

B:

In onderstaand plaatje zijn ook nog de lijnen -y+x=i met i=0,-1,-2...-7 getekend.

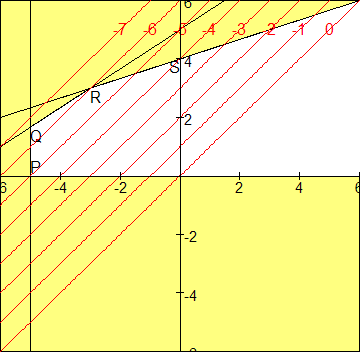
Je kunt hieruit afleiden dat de minimale waarde van -y+x wordt bereikt voor die lijn -y+x=z die gaat door het punt Q. Als je de coordinaten van Q nog niet hebt berekend doe dat dan en vul deze in.

C:
xy=0 betekent: punten in het 2e of 4e kwadrant. Omdat -y0 (dus y0) gaat het om punten in het 2e kwadrant. Weer voldoet het "witte" gebied.

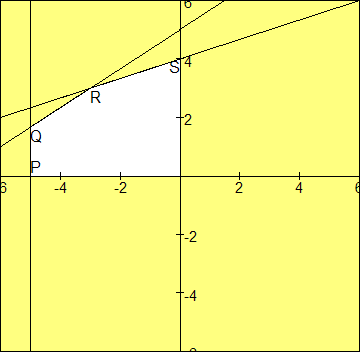
Het gebied bestaat uit twee trapezia als je de verticale lijn door R tekent. De oppervlakte moet dan ook wel lukken.

Dus niet zo'n hele boterham. Meer een pistoletje.

PS de tekeningen zijn gemaakt met Wiskit. Kan ik je aanraden!

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 18 december 2004