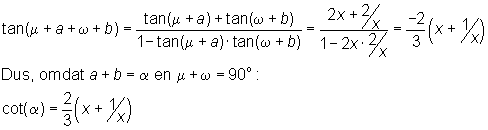WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Driehoek, zwaartlijnen en de tangens

Hallo,

Driehoek met hoekpunten u,v en w zijn gegeven en rechthoekig in u. Men trekt de zwaartelijnen vm en wp die een (scherpe) hoek a vormen. Bepaal nu de tangens van de hoeken v en w, genoteerd in functie van hoek a.
Groeten.
hl
Ouder - vrijdag 17 december 2004

Antwoord

Wat een leuk probleem!
Ik heb het als volgt opgelost:

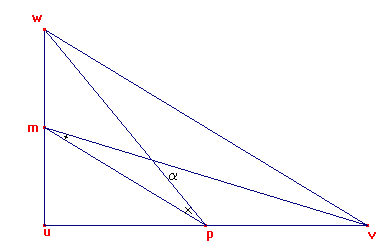
Noem m de hoek bij hoekpunt v.
Noem w de hoek bij hoekpunt w.
Noem x = tan(m)
Dan geldt: ¹/_x = tan(w).
Noem a = Ðwpm en b = Ðvmp
Dan is a + b = a
Verder is Ðupw = m+a en tan(Ðupw) = 2·tan(m) = 2x (vanwege de zwaartelijnen)
en ook tan(Ðumv) = 2·tan(w) = ²/_x
Er geldt:

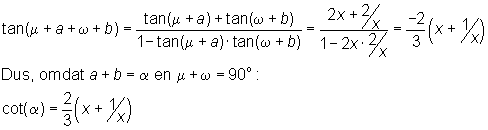
waaruit x eenvoudig is op te lossen.

P.S.
Medebeantwoorder kn heeft nog een alternatieve oplossing:

Neem p=Ðuvm en q=Ðuwp.
Dan is p+q+a=90°.
Dus cot(a)=(tan(p)+tan(q))/(1-tan(p)·tan(q)).
maar tan(p)=(tan(m))/2 en tan(q)=(tan(w))/2.
Invullen levert hetzelfde resultaat als hierboven.

groet,

Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 17 december 2004