WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Grafen vergelijken aan de hand van de matrix

Ik moet een applicatie schrijven die twee willekeurige grafen vergelijkt en moet bepalen of deze grafen isomorf zijn of niet. Ik doe dit op basis van een eerder geschreven applicatie die in een graaf aan de hand van de matrix kan bepalen of er een Eulercircuit of pad bestaat.

Hoe kan ik op basis van de matrix berekenen of twee graven isomorf zijn?

Ik zat te denken aan het vergelijken van de graad van ieder punt. Als in graaf A, met 4 punten, twee punten met een 2de graad voorkomen en twee met een 3de, dan zou dit in graaf B ook zo moeten zijn. Gaat dit altijd op? Is er een algoritme om dit te doen?
Erik V
Student hbo - donderdag 2 december 2004

Antwoord

Als je uitgaat van een directe-wegen-matrix dan zou je moeten laten zien dat de matrices van A en B precies hetzelfde zijn, eventueel door verwisseling van punten. In dat geval zijn de grafen isomorf.

Alleen kijken naar de in- en uitgraad zal niet voldoende zijn. Ligt een directe-wegen-matrix vast bij gegeven in- en uitgraad? Een voorbeeld:

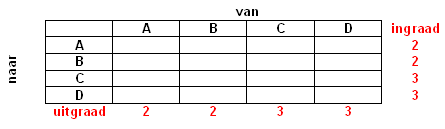
Ligt nu de matrix vast? Ik denk het niet! Dit laat zich eenvoudig demonstreren:

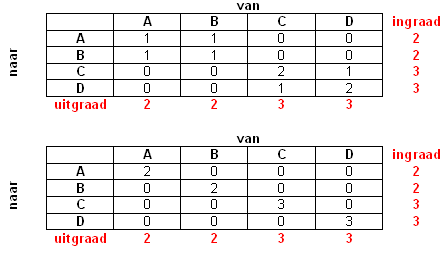
Twee verschillende grafen met dezelfde in- en uitgraad! Dus dat gaat niet lukken denk ik.

Hoe dan wel? Ik zou, denk ik, kiezen voor de volgende aanpak:
Evenveel punten? Nee? Dan niet isomorf!
Evenveel lijnen? Nee? Dan niet isomorf!
Dezelfde in- en uitgraad? Nee? Dan niet isomorf!
Sorteren op in- en uitgraad. Zijn de cellen hetzelfde? Nee? Dan eventueel punten met dezelfde graad stuk voor stuk verwisselen.... en steeds controleren of de cellen hetzelfde zijn? Lukt dat niet? Dan zijn ze niet isomorf!
Lukt het wel? Ja, dan zijn de grafen isomorf...
Hopelijk lukt dat zo...

Je zou natuurlijk ook kunnen kiezen voor de methode om alle mogelijke 'volgorden' te bekijken... lukt het niet een zelfde matrix te vinden, dan zijn de grafen niet isomorf, maar bij veel punten wordt dat misschien toch een beetje een langdurige geschiedenis...

Welnu, er zijn vast wel slimmere dingen te bedenken! Wel aardig om over na te denken... hopelijk kan je weer even verder. Verzin maar 's wat!

Een leuk voorbeeld om te testen of je algoritme werkt kan je vinden op Petersen-graaf.
P.S.
Je maakt van beide grafen de matrix, zeg A en B, en je zoekt of er een permutatiematrix P bestaat zodat P^T·A·P=B. Het nadeel is dat A bijna altijd singulier is, zodat je niet kunt inverteren.

Ander idee: je berekent van A en B ook een aantal machten.
Bij isomorfe grafen verschijnen bij gelijke machten altijd dezelfde getallen, waardoor je de bijectie van de punten gemakkelijk kunt herkennen. Deze methode werkt in praktijkgevallen (nou ja, wat heet praktijk...) best aardig, maar het is geen algoritme.
Boeiend probleem!

Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 2 december 2004