|
|
|
\require{AMSmath}



Verloop van goniometrische functie f(x) = 4cos²x-8cosx+3
Beste,
Als inoefening wou ik het verloop eens willen bepalen van de functie: f(x)=4cos2x-8cosx+3
zou je me soms willen helpen?
domein: je moet eerst de periode bepalen van 4cos2x (wat is de periode hiervan?) en dan van 8cosx (dat is 2p)
snijpunten: doorsnede x-as dus y=0
dus: 4cos2x-8cosx+3=0 maar hoe bepaal je dat???
voor doorsnede y-as: x=0 (wanneer is dat?)
assymptoten: geen aangezien de periodiciteit
eerste afgeleide: (8cosx*(-sinx)) - (8sinx)
hoe bepaal je de nulpunten?
tweede afgeleide: ((-sinx - cosx)- (cosx) Hoe bepaal je de nulpunten?
Kan je zo mijn vragen eens oplossen. En eventueel fouten verbeteren? Want aan de hand van deze oefn gaat het beter lukken bij andere omdat ik zo het systeem kan snappen.
Dank bij voorbaat
Lien
3de graad ASO - donderdag 21 oktober 2004
Antwoord
Domein
Je schrijft dat voor het domein de periode van 4cos2x zou moeten bepalen.
Maar cos(x), en dus ook cos2x, bestaat voor iedere x.
Het grootst mogelijke domein van f is dus de verzameling van de reële getallen.
De functie f is inderdaad periodiek.
Voor de bepaling van een interval waarop alle functiewaardes van f precies één keer worden aangenomen, is de periode van f uiteraard wel nodig.
Die wordt bepaald door de periode van cos(x), en die is inderdaad 2p, en die van cos2x.
Heb je een grafische rekenmachine?
Dan kan je uit de grafiek van cos2x de periode wel bepalen.
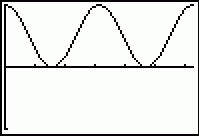
Maar het kan ook anders.
We hebben de formule:
cos(2x) = cos2x - sin2x = cos2x - (1 - cos2x) = 2cos2x - 1
zodat
cos2x = 1/2( cos(2x) + 1 )
En cos(2x) heeft periode p; cos2x dus ook!
Echter jouw functie f heeft een periode 2p, veroorzaakt door ... (ga dat dus zelf na!)
Maxima en minima
Voor het verloop van de functie f zou je eens kunnen kijken naar de functie:
h(t) = 4t2 - 8t + 3
We hebben hier dus cos(x) = t gesteld (dat kan hier, toevallig).
Beschouw de functie h op het domein [-1 ; 1]. Waarom op dit domein?
Als je dan t laat lopen van 1 via 0 naar -1 en weer terug (van -1 via 0 naar 1), vind je de volgende
functiewaardes:
h(1) = -1, h(0) = 3, h(-1) = 15, h(0) = 3, h(1) = -1
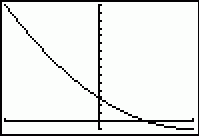
Merk op dat die functiewaardes als je van 1 naar -1 gaat, toenemen, en als je van -1 naar 1 gaat, nemen ze af.
De functie h heeft dus een minimum van -1 en een maximum van 15.
En wat weet je dan ook van de extremen van jouw functie f?
Voor h(t) hebben we ook
h(t) = 4t2 - 2t - 6t + 3 = 2t(2t - 1) - 3(2t - 1) = (2t - 3)(2t - 1)
Het enige nulpunt van h op het interval [-1 ; 1] vinden we dus voor t = 1/2.
En voor t geldt cos(x) = t. Hoe groot is x voor t = 1/2?
Dit geeft de nulpunten van de functie f...
De extreme waarden van de functie f zijn nu ook bekend.
Voor welke waarden van x vind je die? (Wat is x voor t = 1 en voor t = -1?)
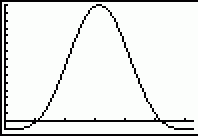 (schets van f op [0; 2p]) (schets van f op [0; 2p])
Asymptoten
Periodiciteit heeft niets met asymptotisch gedrag van een functie te maken; immers tan(x), een periodieke functie, heeft wel degelijk asymptoten.
De functie f is voor elke x gedefinieerd, dus f heeft zeker geen verticale asymptoten.
En uit het gedrag van de functie h volgt ook dat f geen horizontale asymptoten heeft.
Afgeleides
N.B. (cos x)' = -sin x
Dus
f '(x) = 8cos x . -sin x + 8 sin x = 8sin x . (1 - cos x)
Tekenschema van de functie f':
f ': 0+ + + + + + + + + + 0 - - - - - - - - - - 0
x : 0__________________p_______________2p
t : 1__________________-1_______________1 (voor het gemak erbij gezet)
Waarmee je opnieuw de extreme waarden van f kunt berekenen.
Je kan f '(x) schrijven als (formule!):
f '(x) = -4sin(2x) + 8 sin x
Zodat:
f "(x) = -8cos(2x) + 8cos(x)
f "(x) = 0 als cos(2x) = cos(x)
Dus 2x = x (mod 2p) OF 2x = - x (mod 2p); immers de periode van de cosinus is 2p.
N.B. (mod 2p) is hetzelfde als "+ k . 2p".
Hieruit volgt:
Enerzijds:
x = 0 (mod 2p); dus op het domein [0;2p] hebben we x = 0 en x = 2p.
Maar voor deze x'en vinden we geen buigpunten! Waarom niet?
En anderzijds:
3x = 0 (mod 2p), waaruit volgt x = 0 (mod 2/3p).
Hieruit vinden we de buigpunten van de functie, weer op [0;2p], alleen voor x = 2/3p en x = 4/3p.
In jouw uitwerkingen zat nog wel een enkel foutje.
Ik hoop dat je met het bovenstaande wat verder op weg geholpen bent.
Zie voor vervolg Re: Verloop van goniometrische functie f(x) = 4cos²x-8cosx+3.

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 22 oktober 2004
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|










 (schets van f op [0; 2p])
(schets van f op [0; 2p])
