WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Stelsel differentiaalvergelijkingen oplossen

Hallo.

Bepaal de oplossing van het volgende stelsel differentiaalvergelijken.

x'(t) = 3x(t) + z(t)
y'(t) = 3y(t) + z(t)
z'(t) = x(t) + y(t) + 2z(t)

die voldoet aan x(0)= 3 , y(0)= 1 , z(0)= -1.

Ik heb mbv de matrix:

3 0 1
0 3 1
1 1 2

de eigenwaarden en eigenvectoren berekend.
l=1 eigenvector:
1
1
-2

l=3 eigenvector:
1
-1
0

l=4 eigenvector:
1
1
1

Verder dan dit kom ik niet.

Alvast bedankt

Mark
Student hbo - dinsdag 14 september 2004

Antwoord

dag Mark,

de algemene oplossing van het stelsel differentiaalvergelijkingen wordt dan:

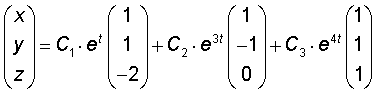
Het berekenen van de constanten laat ik aan jou over.
groet,

Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 14 september 2004

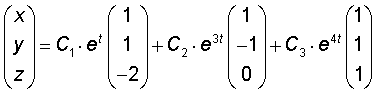
Re: Stelsel differentiaalvergelijkingen oplossen