WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Bewijzen

Beste mevrouw/meneer,

Ik heb twee opgaven waar ik niet zo goed weet wat ik moet doen. Ik hoop dat u mij kunt helpen.

De eerste opgave is de volgende:

Bewijs dat twee rechthoekige driehoeken congruent zijn als ze gelijk hebben: een scherpe hoek en de hoogtelijn op de schuine zijde.

Ik heb een driehoek ABC getekend en op de lijn BC heb ik een lijn getekend die loodrecht staat op dit lijnstuk en door hoek A gaat. Volgens de methode die ik moet hanteren moet je opschrijven wat gegeven is, wat je moet bewijzen en het bewijs. Ik weet niet hoe je met hetgeen je opschrijft onder het kopje wat gegeven is het bewijs kunt leveren.

De tweede opgave waar ik niet mee uit de voeten kan is de volgende:

Door het hoekpunt C van driehoek ABC wordt een lijn l getekend evenwijdig aan AB. Op l wordt een stuk CE=AB afgepast, waarbij E en B aan weerszijden van AC liggen. Nu moet je bewijzen dat BE en AC elkaar middendoor delen.

Ik heb aan de hand van deze gegevens een tekening gemaakt. Uit deze tekening blijkt dat BE en AC elkaar inderdaad middendoor delen. Opnieuw moet ik werken volgens het stappenplan wat gegeven is, te bewijzen en het bewijs. Onder het kopje gegeven heb ik geschreven CE=AB. Onder het kopje bewijs heb ik geschreven AB=CE
ÐS1=ÐS2
ÐS3=ÐS4
Ik weet nu niet hoe ik verder moet.

Ik hoop dat u mij met beide opgaven kunt helpen.

Alvast ontzettend bedankt.
Brecht
Student hbo - zaterdag 4 september 2004

Antwoord

Inderdaad een tekening is handig. Maar er is meer! En dan bedoel ik dat je ook de consequenties van de gegevens bekijkt.
Allereerst maar eens je eerste probleem (zie figuur 1).
Laten we aannemen dat die gelijke scherpe hoeken (ze kunnen overigens niet stomp zijn..) de hoeken B en B' zijn.
En je weet dat AD en A'D' gelijk zijn.
Kijk nu eens naar de driehoeken ABD en A'B'D'.
Wat weet je van de hoeken A₁ en A'₁ daarin?
Kan je nu bewijzen dat díe driehoeken congruent zijn?
En dan kan je daaruit wel iets afleiden over AB en A'B'.
En hoeveel elementen van de driehoeken ABC en A'B'C' zijn er nu gelijk?
Enneh, wat gegeven is heb je eigenlijk al in deze vraag weergegeven, maar kort opgeschreven:
Gegeven:
DABC en DA'B'C' met ÐB = ÐB',
AD en A'D' zijn hoogtelijnen, met AD = A'D
Te bewijzen:
DABC @ DA'B'C'
Het bewijs kan je nu denk ik wel afleiden via het bovenstaande (gebruik zo weinig mogelijk woorden).

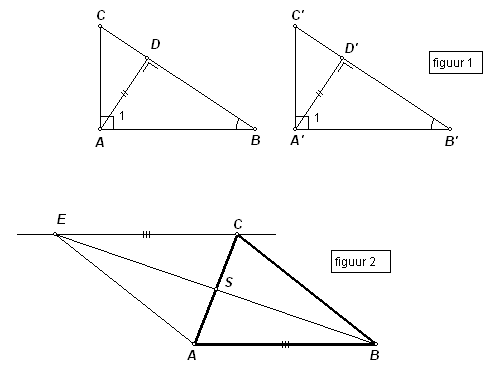
En dan je tweede vraag (zie figuur 2).
Ik denk dat je het wat te ver zoekt.
Gegeven is ook dat CE // AB. Dat moet je dus gebruiken!
Bekijk de vierhoek ABCE.
Wat weet je van AB en CE? Volgens mij twee dingen...
Dan weet je ook dat die vierhoek een ... (tja, invullen) is.
En in een ... delen de diagonalen (en dat zijn BE en AC van die vierhoek) elkaar middendoor delen.

Zo genoeg geholpen? Ik vind van wel.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 4 september 2004