WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Standaarddeviatie normale verdeling CasioCFX-9850

Een boomkweker koopt een grote partij jonge sparreboompjes. Uit onderzoek is bekend dat de lengte van jonge sparreboompjes normaal verdeeld is met een gemiddelde van 25cm en dat 5% van de boompjes korter is dan 20 cm.
Bereken de standaard afwijking van de lengteverdeling.
Kan iemand mij uitleggen hoe ik dat moet doen?

BRON: EXAMEN - HAVO wiskunde B1 - 2003 - 1e tijdvak
kasper
Cursist vavo - maandag 21 juni 2004

Antwoord

Je kunt proberen d.m.v. Trial & Error de standaarddeviatie te bepalen. Op Casio 9850 en de normale verdeling staat dat uitgelegd.

Je kunt ook de standaard normale verdeling gebruiken. Ik zal dat nog eens voor doen...

Ik weet het volgende:

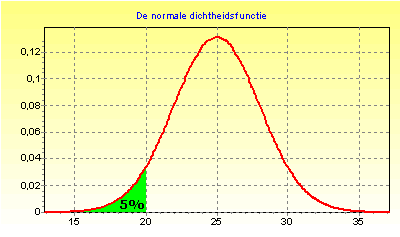
Het probleem is nu dat we met die CASIO alleen maar ofwel de kans kunnen bereken als je het gemiddelde, de standaarddeiviatie en de grenzen kent OF de grenswaarde als je het gemiddelde, de standaarddeviatie en de kans kent.

Van de standaard normale verdeling weten we wel alles! Je weet dat het gemiddelde nul is en de standaarddeviatie 1. Dat betekent dat je voor elke grenswaarde de kans kunt berekenen en voor elke kans de grenswaarde.

Hetzelfde probleem als hierboven met de standaardnormale verdeling:

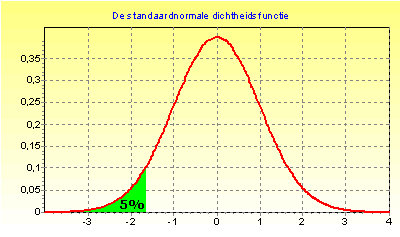
Met invNorm kun je nu precies uitrekenen welke z-score er hoort bij 5%. Het blijkt z=-1,6448535

Gebruik dan de formule op je formulekaart:

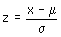
Als je nu invult wat je weet krijg je een vergelijking met 1 onbekende (de standaarddeviatie!) en deze vergelijking kan je oplossen en dan ben je er...

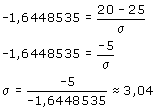
Een heel gedoe... maar ook toepasbaar als je bijvoorbeeld het gemiddelde niet kent.

Hopelijk helpt dat.

P.S.
Opmerkelijk is dat in het correctievoorschrift als antwoord staat 3,05. Dit komt door de afronding van z=-1,64 Komt dat uit een tabel? Of uit de GR? Twee decimalen is dus een beetje onzin! Ze hadden beter 1 decimaal kunnen vragen.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 21 juni 2004

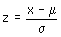
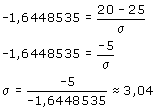
Re: Standaarddeviatie normale verdeling CasioCFX-9850