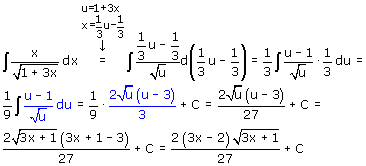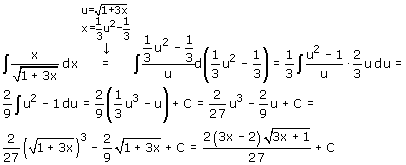WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Lastige integraal met substitutie

Hallo,

De volgende integraal loop ik vast. òxÖ(1+3x)dx
Het volgende heb ik bedacht: ik moet een de volgende vorm krijgen. (1+3x)Ö(1+3x)d(1+3x). Dan kan je 1+3x vervangen voor u. d(1+3x)=3dx dus,
3(1+3x)Ö(1+3x)dx daarna de vorm met 1/9 vermenigvuldigen -- 1/9*3(1+3x)Ö(1+3x)dx maar dat is een constante van 1/3 te veel.

Dus 1/9*3(1+3x)Ö(1+3x)-1/3 dx. Is dit fout gedacht? Dit is denk is gelijk aan xÖ(1+3x)dx. Dus krijg de volgende vorm 1/9(1+3x)Ö(1+3x)-1/3 d(1+3x), nu kan je schrijven 1/9uÖu-1/3 du = d(2/45u²Öu-1/3u).
met u=(1+3x). Maar de primitieve is fout want als 'k weer de afgeleide bepaal dan krijg 'k 1/3+xÖ(1+3x)-1. De constante is niet goed. Kom er niet uit.
Kan iemand me misschien helpen?

Bedank! GrJasper
Jasper
Student hbo - vrijdag 7 mei 2004

Antwoord

Ik geloof niet dat ik dit helemaal volg. Maar met de substitie u=1+3x krijg ik:

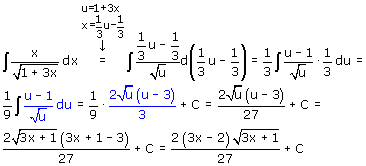
..en dat is allemaal wel mogelijk, maar bij het blauwe stuk zit toch iets eigenaardigs...!?

Zelf zou ik kiezen voor de substitutie u=Ö(1+3x). Je krijgt dan:

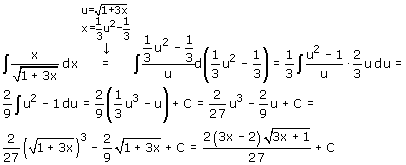
Waarbij misschien de laatste stap een beetje lastig is, misschien, maar verder goed te doen, lijkt me. In feit gebruik ik daarbij de Omgekeerde toepassing van de substitutiemethode. Nou ja, kijk maar of je er iets mee kan.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 7 mei 2004