WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Bgsinx

Hallo,
kunt U me aub. met volgende vgl. helpen:
1) Bgsinx=Bgsin(4/5)+Bgsin(3/5)
2) Bgtg(x+1)+Bgcotg(x-1)=Bgsin(4/5)+Bgcos(3/5)

Bedankt.
Karina
Student universiteit België - dinsdag 9 maart 2004

Antwoord

dag Karina,

Ik neem aan dat de genoemde vergelijkingen moeten worden opgelost. Er is een slimme aanpak, en een die gewoon stug rekent.

Eerst de methode voor als je de slimme aanpak niet ziet...
Hiervoor is enige kennis van goniometrische formules handig,

bijvoorbeeld
sin(a+b)=sin(a)·cos(b) + cos(a)·sin(b)

Verder moet je bijvoorbeeld cos(bgsin(a)) kunnen uitrekenen.
Dat gaat met behulp van een rechthoekige driehoek, waarin je de hoek bgsin(a) neerzet, en daarmee geschikte waarden voor de overstaande en schuine zijden kiest. Dan kun je met de stelling van Pythagoras de andere zijde berekenen, en dus ook cos(bgsin(a))

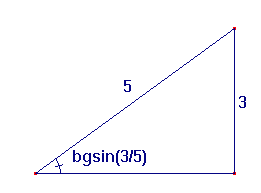
Hiermee moet je nu in staat zijn om je eerste vergelijking op te lossen.

Maar: het kan dus ook slimmer.

Uit hetzelfde plaatje kun je direct zien, dat
bgsin(4/5)+ bgsin(3/5) = $\pi$/2. waarmee de vergelijking wel erg eenvoudig wordt!

Voor de tweede vergelijking kun je gebruikmaken van het feit, dat bgcotg(a) gelijk is aan $\pi$/2 - bgtan(a)
en dat bgsin(4/5) gelijk is aan bgcos(3/5) (zie plaatje).

Verder kun je de regel gebruiken:

tan(a-b) = (tan(a)-tan(b))/(1+tan(a)·tan(b))

en dan moet je er ook uitkomen, hoop ik. Anders hoor ik het nog wel.

Succes!

Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 9 maart 2004