WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Probleem van de forens

Een forens wordt dagelijks door zijn vrouw van de trein gehaald. Op een zekere dag neemt hij een trein die een uur eerder gaat. Zijn vrouw weet dat niet en staat dus niet bij het station. Hij besluit vast naar huis te gaan lopen. Zijn vrouw vertrekt op de gewone tijd en komt hem onderweg tegen. Hij stapt in en samen gaan ze naar huis. Ze komen 10 minuten eerder thuis dan gewoonlijk. we gaan van constante snelheden uit.

Hoe lang heeft hij gewandeld?
hub
Student hbo - maandag 9 februari 2004

Antwoord

Hoi,

We veronderstellen dat zijn vrouw normaal aankomt aan het station op het moment dat hij met de trein aankomt. Volgend plaatje is het tijd-afstand-diagram.

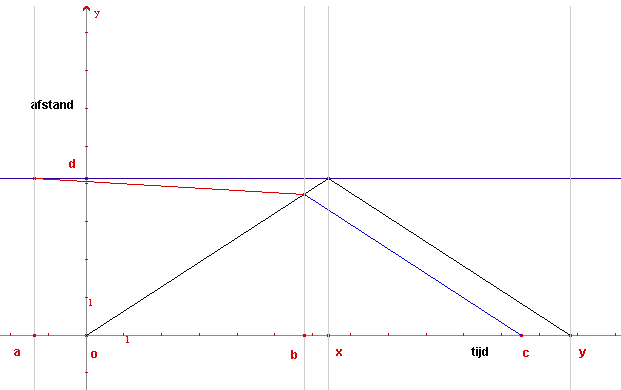
Het station ligt op een afstand d van de woning van het koppel.

De tijdstippen:
o: vrouw vertrekt
x: vrouw komt aan bij station en pikt haar man op - normale uurregeling
y: vrouw en man komen samen thuis - normale uurregeling
a: man vertrekt te voet bij station
b: man ontmoet te voet zijn vrouw en keren samen huiswaarts in wagen
c: man en vrouw komen samen thuis nadat man te voet naderde

We hebben:
y=2x
b/c=x/y en dus c=2b
x-a=60min
y-c=10min

Gevraagd: b-a ?
y-c=2x-2b=10min, dus is x-b=5min. Met x-a=60min vinden we dat b-a=55min. Het leuke is dat dit onafhankelijk is van x en d en dat de snelheid van de wagen, de man en de afstand tot het station dus geen rol spelen. Er is wel een verband tussen de snelheid van de man en die van de vrouw. Reken je die eens na?

Groetjes,
Johan

andros

Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 9 februari 2004

Re: Probleem van de forens