|
|
|
\require{AMSmath}



Bicentrisch trapezium
Een bicentrische vierhoek is een vierhoek met een omgeschreven én een ingeschreven cirkel: koordenvierhoek én raaklijnenvierhoek ineen.
Eenvoudig te bewijzen is dat een bicentrisch trapezium gelijkbenig is.
Ik 'worstel' nu al enkele dagen met het volgende probleem.
Gegeven de omcirkel en de grootste van de beide evenwijdige zijden van het trapezium.
Construeer nu "met passer en liniaal" het bicentrisch trapezium".
Ik maak jullie medebeantwoorders dus deelgenoot van mijn probleem, waarbij ik meld dat het probleem in ieder geval oplosbaar is door de snijpunten van een cirkel en een parabool te bepalen.
Ik houd me dus aanbevolen voor een passer-en-liniaal-constructie of voor een onmogelijkheidsbewijs van een dergelijke constructie.
Dick K
Beantwoorder - vrijdag 23 januari 2004
Antwoord
(van de vragensteller zelf)
Een trapezium RSPQ met zijden a+a, a+b, b+b, b+a (a b) heeft steeds een incirkel. b) heeft steeds een incirkel.
Terzijde: de straal van de incirkel is Ö(ab).
De lengte van de middenparallel van een bicentrisch trapezium is gelijk aan de lengte van de opstaande zijde!
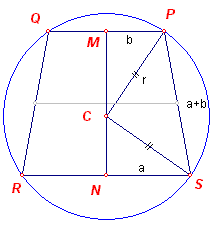
Stel (C,r) is de omcirkel van RSPQ.
N en M zijn opvolgend de middens van de zijden RS en PQ.
De cosinusregel in middelpuntsdriehoek PCS (met zijden r, a+b, r) geeft:
(a+b)2 - 2r2 = -2r2·cos(PCS)
Maar ook (in de driehoeken PCM en SCN met gebruik van de somformule voor de cosinus):
-2r2·cos(PCS) = +2r2·cos(PCM + SCN) = 2Ö(r2-a2)·Ö(r2-b2) - 2ab
Zodat
(a+b)2 - 2r2 = 2Ö(r2-a2)·Ö(r2-b2) - 2ab
Bij gegeven a en r staat hier (na 'wat' kwadrateren) een vierdegraadsvergelijking in b.
En blijkbaar (*) is deze vergelijking irreducibel (niet te onbinden in factoren met lagere graad).
b is danook niet te construeren met passer en liniaal, bij gegeven a en r.
(*)
Dit werd gemeld door Jean-Pierre Ehrmann (Frankrijk), nadat ik dezelfde vraag had voorgelegd aan Hyacinthos, een internationale discussiegroep over driehoeksmeetkunde.
Uit de Galois-theorie (een niet erg eenvoudig onderdeel van de algebra) blijkt namelijk, dat de groep die aan deze vergelijking gekoppeld kan worden, de Galois-groep S4 is (en daaruit volgt dan de irreducibiliteit...).
Met dank aan Anneke, Floor (FvL) en Aad Goddijn (aad) die zich met mij over dit probleem hebben gebogen.
Floor en Aad bevestigden (met Maple) de Galois-groep S4 bij dit probleem.
Zoals in de vraag is opgemerkt, is het probleem wel 'Cabri-construeerbaar': door gebruik te maken van een parabool (die in Cabri eenvoudig te tekenen is).
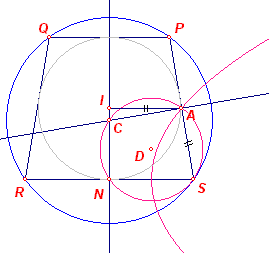
Het midden A van PS ligt op een Thales-cirkel met middellijn CS, immers C ligt op de middelloodlijn van PS.
Voorts is IA = AS (I is het middelpunt van de incirkel). A ligt dus op de parabool met S als brandpunt en de middelloodlijn van RS als richtlijn.
Het punt A kan dus als snijpunt van cirkel en parabool eenvoudig worden gevonden. En dan volgen P en Q (en de incirkel) snel daarna.
N.B. Het probleem heeft twee oplossingen. Zie het tweede snijpunt van de Thales-cirkel en de parabool in bovenstaande figuur.

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 29 januari 2004
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|








 b) heeft steeds een incirkel.
b) heeft steeds een incirkel.



 Re: Bicentrisch trapezium
Re: Bicentrisch trapezium