WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Insluitingsstelling

goeiedag,

hoe kun je bewijzen dat de limiet van sin x / x gelijk is aan 1?
gotela
Student Hoger Onderwijs België - dinsdag 13 januari 2004

Antwoord

Aanpak 1
Zie onderstaande figuur

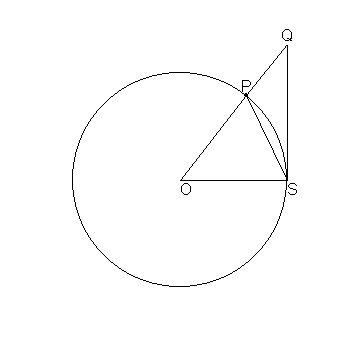
hoek POS=t
De straal van de cirkel is 1
QS^OS
De oppervlakte van driehoek OSP=¹/₂OS*OP*sin(t)=¹/₂sin(t)
De oppervlakte van sector OSP=t/(2p)*Opp cirkel=¹/₂t
De oppervlakte van driehoek OSQ=¹/₂*tan(t)=¹/₂*sin(t)/cos(t)

opp driehoek(OSP)opp sector(OSP)opp driehoek(OSQ),

dus ¹/₂sin(t)¹/₂t¹/₂sin(t)/cos(t)
Vermenigvuldigen met 2 en omkering van de termen geeft:
1/sin(t)1/tcos(t)/sin(t)
Vermenigvuldigen met sin(t) (t0) geeft:
1sin(t)/tcos(t).
Deze ongelijkheid geldt ook voor -¹/₂pt0,
want cos(-t)=cos(t)
en sin(-t)/-t=-sin(t)/-t=sin(t)/t
omdat cos(t) tot 1 nadert als t nadert tot nul geldt nu volgens de insluitstelling de gevraagde limiet.

aanpak 2
Kies f(x)=sin(x), f'(x)=cos(x).
f'(0)=1
lim_t®0(f(t)-f(0))/(t-0)=f'(0)=1

Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 13 januari 2004